What is the relationship between given coordinates, scale, and obtained coordinates?

Question

I have a pgfshape declared as

\pgfdeclareshape{Curve1}{
\inheritsavedanchors[from=coordinate]
\inheritanchor[from=coordinate]{center}
\backgroundpath{
\begin{pgfscope}
\pgftransformshift{\centerpoint}
\pgfmathdivide{\pgfkeysvalueof{/pgf/minimum width}}{1pt}
\pgftransformscale{\pgfmathresult}
\pgfpathmoveto{\pgfpoint{                     0}{                    0}}
[...]
\pgfpathlineto{\pgfpoint{-1.637140473757006e-01}{9.752876882003444e-01}}
[...]
\pgfpathlineto{\pgfpoint{                     0}{                    0}}
\pgfpathclose
\end{pgfscope}}}

where the [...] are ellipsis to indicate several points I've omitted for brevity.

Yet, when I plot it with

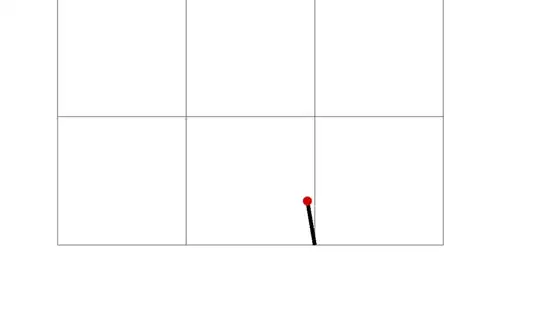
\node [Curve1, draw, scale = 10] at (0, 0) {};

the final location has nothing to do with the 10 * (-1.637140473757006e-01, 9.752876882003444e-01) that I was expecting:

MWE:

\documentclass[english]{scrbook}

\usepackage{tikz}

\pgfdeclareshape{Curve1}{
\inheritsavedanchors[from=coordinate]
\inheritanchor[from=coordinate]{center}
\backgroundpath{
\begin{pgfscope}
\pgftransformshift{\centerpoint}
\pgfmathdivide{\pgfkeysvalueof{/pgf/minimum width}}{1pt}
\pgftransformscale{\pgfmathresult}
\pgfpathmoveto{\pgfpoint{                     0}{                    0}}
\pgfpathlineto{\pgfpoint{-1.637140473757006e-01}{9.752876882003444e-01}}
\pgfpathlineto{\pgfpoint{                     0}{                    0}}
\pgfpathclose
\end{pgfscope}}}

\begin{document}
\begin{figure}
\centering
\begin{tikzpicture}
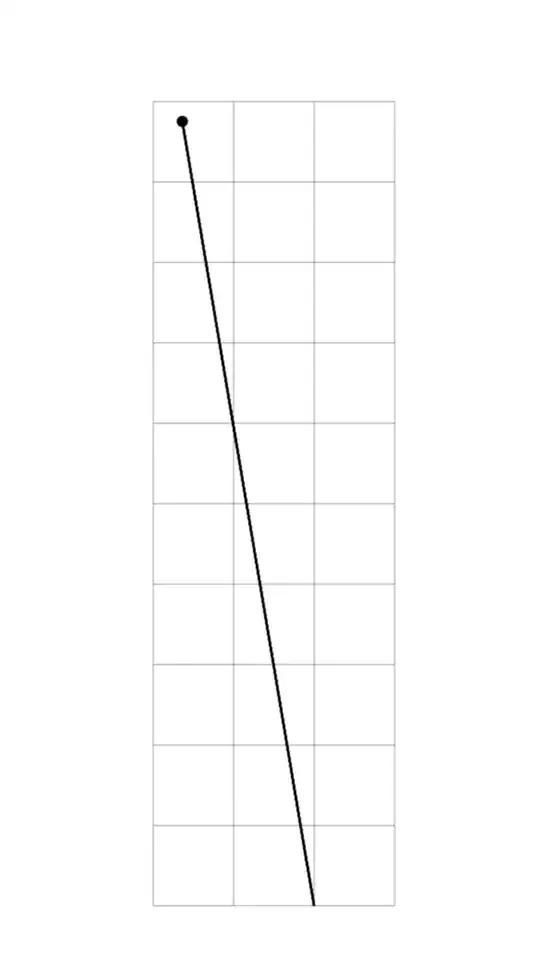
\draw[step=1cm,gray,very thin] (-2,0) grid (1,10);
\node [Curve1, draw, scale = 10, thick] at (0, 0) {};
\fill (-1.637140473757006, 9.752876882003444) circle[radius=2pt];
\end{tikzpicture}
\end{figure}
\end{document}

What is the relationship between the coordinates given in the shape declaration, the scale, and the coordinates in the final picture? Is there a formula I can use somewhere?

Answer 1

You need to remember that commands like \pgfpoint add the units pt if you do not supply them with units. I added a red circle to show that your approach works in principle.

\documentclass[english]{scrbook}

\usepackage{tikz}

\pgfdeclareshape{Curve1}{
\inheritsavedanchors[from=coordinate]
\inheritanchor[from=coordinate]{center}
\backgroundpath{
\begin{pgfscope}
\pgftransformshift{\centerpoint}
\pgfmathdivide{\pgfkeysvalueof{/pgf/minimum width}}{1pt}
\pgftransformscale{\pgfmathresult}
\pgfpathmoveto{\pgfpoint{                     0}{                    0}}
\pgfpathlineto{\pgfpoint{-1.637140473757006e-01}{9.752876882003444e-01}}
\pgfpathlineto{\pgfpoint{                     0}{                    0}}
\pgfpathclose
\end{pgfscope}}}

\begin{document}
\begin{figure}
\centering
\begin{tikzpicture}
\draw[step=1cm,gray,very thin] (-2,0) grid (1,10);
\node [Curve1, draw, scale = 10, thick] at (0, 0) {};
\fill (-1.637140473757006, 9.752876882003444) circle[radius=2pt];
\fill[red] (-1.637140473757006pt, 9.752876882003444pt) circle[radius=1pt];
\end{tikzpicture}
\end{figure}
\end{document}

You can use cm in the declaration of the shape.

\documentclass[english]{scrbook}

\usepackage{tikz}

\pgfdeclareshape{Curve1}{
\inheritsavedanchors[from=coordinate]
\inheritanchor[from=coordinate]{center}
\backgroundpath{
\begin{pgfscope}
\pgftransformshift{\centerpoint}
\pgfmathdivide{\pgfkeysvalueof{/pgf/minimum width}}{1pt}
\pgftransformscale{\pgfmathresult}
\pgfpathmoveto{\pgfpoint{                     0}{                    0}}
\pgfpathlineto{\pgfpoint{-1.637140473757006e-01*1cm}{9.752876882003444e-01*1cm}}
\pgfpathlineto{\pgfpoint{                     0}{                    0}}
\pgfpathclose
\end{pgfscope}}}

\begin{document}
\begin{figure}
\centering
\begin{tikzpicture}
\draw[step=1cm,gray,very thin] (-2,0) grid (1,10);
\node [Curve1, draw, scale = 10, thick] at (0, 0) {};
\fill (-1.637140473757006, 9.752876882003444) circle[radius=2pt];
\end{tikzpicture}
\end{figure}
\end{document}