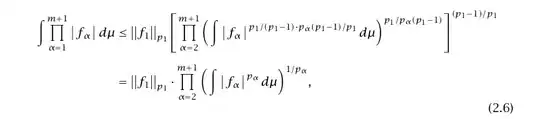Justify of equation to better explanation

Question

I am trying to create pure inequality like this

But I have:

\documentclass{article}

\usepackage{amsmath}

\begin{document}
\[
\int{\prod_{i=1}^{m+1}|f_{i}|d\mu} \leq 
||f_{1}||_{p_{1}}
\left[ 
\prod_{i=2}^{m+1}
    \left(
        \int|f_{i}|^{p_{1}/(p_{1}-1) p_{i}(p_{1}-1)/p_{1}}d\mu
    \right)^{p_{1}/p_{i}(p_{1}-1)}
\right]^{(p_{1}-1)/p_{1}}
\]

\[
= ||f_{1}||_{p_{1}}
\prod_{i=2}^{m+1}
    \left(
        \int|f_{i}|^{p_{i}} d\mu
    \right)^{\frac{1}{p_{i}}}
\]

\end{document}

Answer 1

Some suggestions:

• use an align environment to contain both rows of the display-math material

• use a \notag instruction in the first row to suppress the typesetting of an equation number

• use \biggl and \biggr for all large parentheses and brackets

• load the mathtools package -- a superset of the amsmath package -- and define macros called \abs and \norm. This'll make reading the input code much easier

• optional: place brackets around the exponent of \abs{f_i} to help readers figure out what's going on

\documentclass{article}
\usepackage{mathtools} % for '\DeclarePairedDelimiter' macro
\DeclarePairedDelimiter\abs\lvert\rvert
\DeclarePairedDelimiter\norm\lVert\rVert

\begin{document}
\begin{align}
\int \prod_{i=1}^{m+1} \abs{f_{i}}\,d\mu
&\leq  \norm{f_{1}}_{p_{1}}
\biggl[\, 
\prod_{i=2}^{m+1}
    \biggl(
    \int|f_{i}|^{[p_{1}/(p_{1}-1) p_{i}(p_{1}-1)/p_{1}]}\,d\mu
    \biggr)^{\!p_{1}/p_{i}(p_{1}-1)}
\,\biggr]^{(p_{1}-1)/p_{1}}\notag\\
&= \norm{f_{1}}_{p_{1}}
\prod_{i=2}^{m+1}
    \biggl(
    \int|f_{i}|^{p_{i}} \,d\mu
    \biggr)^{\!1/p_{i}}
\end{align}
\end{document}

Answer 2

With the help of split and a slightly smaller margin using the geometry package you can achieve the following output:

\documentclass{article}
\usepackage{geometry}
\usepackage{amsmath}

\begin{document}
\begin{equation}
\begin{split}
\int{\prod_{i=1}^{m+1}|f_{i}|d\mu} &\leq 
\|f_{1}\|_{p_{1}}
\left[ 
\prod_{i=2}^{m+1}
    \left(
        \int|f_{i}|^{p_{1}/(p_{1}-1) p_{i}(p_{1}-1)/p_{1}}d\mu
    \right)^{p_{1}/p_{i}(p_{1}-1)}
\right]^{(p_{1}-1)/p_{1}}\\
&= \|f_{1}\|_{p_{1}}
\prod_{i=2}^{m+1}
    \left(
        \int|f_{i}|^{p_{i}} d\mu
    \right)^{\frac{1}{p_{i}}}
    \end{split}
\end{equation}

\end{document}