PGF Plots Complex Numbers

Question

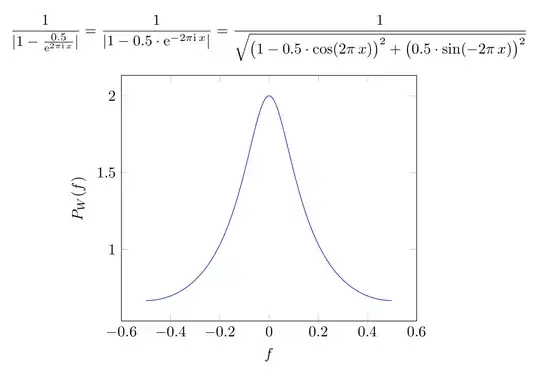
I have the following PGF Plot

\begin{tikzpicture}
\begin{axis}[
xlabel={$f$},
ylabel={$P_{W}(f)$},
%ytick={0.6,0.8,...,2},
%ymin=0,
%ymax=0.4,
]
\addplot[domain=-0.5:0.5,color=blue,samples=100]{1/(abs(1-(0.5/(e^(2*sqrt(1)*pi*x)))))};
\end{axis}
\end{tikzpicture}

the sqrt(1) is supposed to be a complex number, so sqrt(-1) or "i". But PGF Plot doesn't seem to be able to calculate this. How can I do this in PGFPlot?

Since you are interested in the abs value (which is real), you can evaluate it first and then plot. — nidhin, Oct 15 '19 at 13:15
Out of curiosity, is there anything (embeddable or dedicated TeX macro package) that coud allow working with complex numbers? — Tomáš Kruliš, Oct 15 '19 at 13:58

score 2 · Accepted Answer · answered Oct 15 '19 at 13:54

You can do it by hand.

\documentclass[tikz,border=3mm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\begin{tikzpicture}
\begin{axis}[trig format plots=rad,
title={$\displaystyle\frac{1}{|1-\frac{0.5}{\mathrm{e}^{2\pi\mathrm{i}\,x}}|}
=\frac{1}{|1-0.5\cdot\mathrm{e}^{-2\pi\mathrm{i}\,x}|}
=\frac{1}{\sqrt{\bigl(1-0.5\cdot\cos(2\pi\,x)\bigr)^2+\bigl(0.5\cdot
\sin(-2\pi\,x)\bigr)^2}}$},
xlabel={$f$},
ylabel={$P_{W}(f)$}]
\addplot[domain=-0.5:0.5,color=blue,samples=100]{%
1/(sqrt((1-0.5*cos(2*pi*x))^2+(-0.5*sin(2*pi*x))^2))};
\end{axis}
\end{tikzpicture}
\end{document}

PGF Plots Complex Numbers

1 Answers1

Linked