Your setup already has the property alpha=beta. Here is a revised version that addresses the clarification in the comment.
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,angles,quotes}
\begin{document}
\begin{tikzpicture}[scale=2]
\tikzset{dot/.style={circle,inner sep=1pt,fill,label={#1},name=#1},
extended line/.style={shorten >=-#1,shorten <=-#1},
extended line/.default=1cm
}
\pgfmathsetmacro\r{1}
\coordinate (O) at (-2,1);
\path (O) -- ++(130:\r) coordinate (A)
(O) -- ++(30:\r) coordinate (B)
(O) -- ++(-90:\r) coordinate (C)
;
\path let \p1=($(B)-(A)$),\p2=($(C)-(A)$),
\p3=($(B)-(C)$),\n1={-atan2(\y1,\x1)+atan2(\y2,\x2)+atan2(\y3,\x3)}
in ($(C)+(\n1:2)$) coordinate (D);
\draw (O) circle (\r);
\draw (A) -- (B) -- (C) -- cycle
let \p1=($(B)-(A)$),\p2=($(C)-(A)$),
\p3=($(B)-(C)$),\p4=($(D)-(C)$),
\n1={atan2(\y1,\x1)-atan2(\y2,\x2)},
\n2={atan2(\y3,\x3)-atan2(\y4,\x4)} in
pic["$\alpha=\pgfmathparse{\n1}\pgfmathprintnumber\pgfmathresult$"
{anchor=160},draw,angle eccentricity=1.8,angle radius=6] {angle=C--A--B}
pic["$\beta=\pgfmathparse{\n2}\pgfmathprintnumber\pgfmathresult$"
{anchor=200}
,draw,angle eccentricity=1.8,angle radius=6] {angle=D--C--B};
\draw[red,extended line=2cm] (C) -- (D);
\foreach \x in {A,B,C,D,O} {
\node[circle,fill,inner sep=0,minimum size=2pt,label=$\x$] at (\x) {};
}
\end{tikzpicture}
\end{document}

An animation:
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,angles,quotes,through}
\tikzset{circle through 3 points/.style n args={3}{% https://tex.stackexchange.com/a/461180
insert path={let \p1=($(#1)!0.5!(#2)$),
\p2=($(#1)!0.5!(#3)$),
\p3=($(#1)!0.5!(#2)!1!-90:(#2)$),
\p4=($(#1)!0.5!(#3)!1!90:(#3)$),
\p5=(intersection of \p1--\p3 and \p2--\p4)
in },
at={(\p5)},
circle through= {(#1)}
}}
\begin{document}
\tikzset{dot/.style={circle,inner sep=1pt,fill,label={#1},name=#1},
extended line/.style={shorten >=-#1,shorten <=-#1},
extended line/.default=1cm
}
\foreach \X in {1,1.1,...,2,1.9,1.8,...,1.1}
{\begin{tikzpicture}[scale=2]
\pgfmathsetmacro\r{1}
\path[use as bounding box] (-4,3) rectangle (1,-0.3); % for animation
\coordinate (O) at (-2,1);
\path (O) -- ++(130:\X*\r) coordinate (A)
(O) -- ++(30:\r) coordinate (B)
(O) -- ++(-90:\r) coordinate (C)
;
\path let \p1=($(B)-(A)$),\p2=($(C)-(A)$),
\p3=($(B)-(C)$),\n1={-atan2(\y1,\x1)+atan2(\y2,\x2)+atan2(\y3,\x3)}
in ($(C)+(\n1:2)$) coordinate (D);
\draw[gray,thin] (O) circle (\r);
\node[circle through 3 points={A}{B}{C},draw=blue](O'){};
\draw (A) -- (B) -- (C) -- cycle
let \p1=($(B)-(A)$),\p2=($(C)-(A)$),
\p3=($(B)-(C)$),\p4=($(D)-(C)$),
\n1={atan2(\y1,\x1)-atan2(\y2,\x2)},
\n2={atan2(\y3,\x3)-atan2(\y4,\x4)} in
pic["$\alpha=\pgfmathparse{\n1}\pgfmathprintnumber\pgfmathresult$"
{anchor=160},draw,angle eccentricity=1.8,angle radius=6] {angle=C--A--B}
pic["$\beta=\pgfmathparse{\n2}\pgfmathprintnumber\pgfmathresult$"
{anchor=200}
,draw,angle eccentricity=1.8,angle radius=6] {angle=D--C--B};
\draw[red,extended line=2cm] (C) -- (D);
\foreach \x in {A,B,C,D,O,O'} {
\node[circle,fill,inner sep=0,minimum size=2pt,label=$\x$] at (\x) {};
}
\end{tikzpicture}}
\end{document}
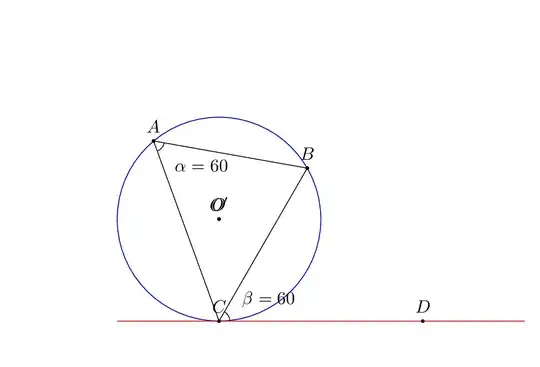
 (current D point should be changed)
(current D point should be changed)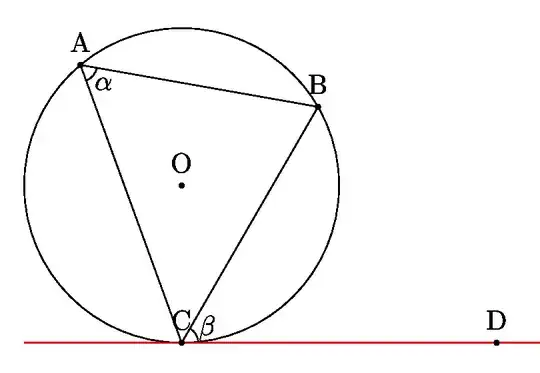


A,BandCon the circle? And why do you suggest to moveAoutside the circle? – Oct 20 '19 at 10:02