I had a similar question regarding a torus combined with an arc for the particle trajectory here.
With the nice and very helpful support by Schrödinger's cat, I managed to produce the desired plot. Now, I'm trying the same with a cone, inspired by this sketch:
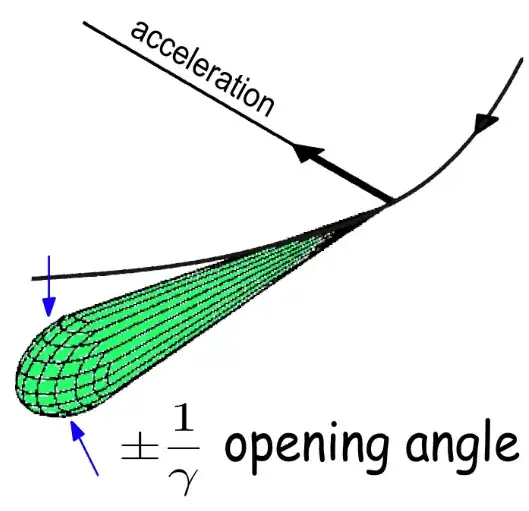
Based on the solution to my former question, I managed a basic setup:
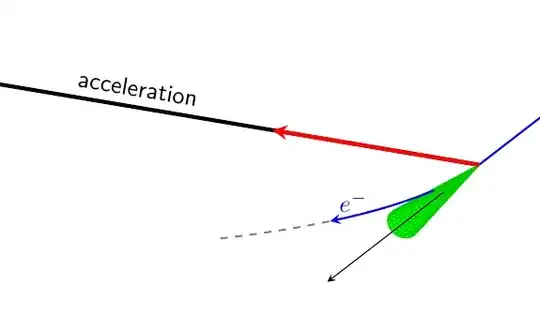
\documentclass[a4paper,10pt]{article}
\usepackage[utf8]{inputenc}
\usepackage[dvipsnames]{xcolor}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\usetikzlibrary{3d,backgrounds,calc}
\begin{document}
\begin{tikzpicture}[thkline/.style={thick, blue, >=stealth},font=\sffamily]
\begin{axis}[anchor=origin,
xmax=15, ymax=15, zmax=10, axis lines = none,
domain=0:15,
colormap={green}{color=(green) color=(green)},
clip=false]
%background stuff
\draw[ultra thick] (0,0,0) coordinate(O) -- (-25,0,0)
node[pos=2/3,above,sloped]{acceleration};
\path let \p1=($(1,0,0)-(0,0,0)$),\p2=($(0,1,0)-(0,0,0)$),
\p3=($(0,0,1)-(0,0,0)$) in
\pgfextra{\xdef\myxx{\x1}\xdef\myxy{\y1}
\xdef\myyx{\x2}\xdef\myyy{\y2}
\xdef\myzx{\x3}\xdef\myzy{\y3}};
% torus
\addplot3[surf, y domain=0:360]
( {x/20*cos(y)},
-{x},
{x/20*sin(y)} );
% foreground
\begin{scope}[canvas is xy plane at z=0,>=stealth]
\end{scope}
\end{axis}
\begin{scope}[x={(\myxx,\myxy)},y={(\myyx,\myyy)},z={(\myzx,\myzy)},
canvas is xy plane at z=0,>=stealth,on background layer]
\pgflowlevelsynccm
\draw[thick,blue] (0,30) -- (0,0);
\draw[->,blue] (0,30) -- (0,20);
\draw[->] (0,0) coordinate(O) -- (0,-7);
\draw[thick,dashed,gray] (0,0) arc(0:-30:50);
\end{scope}
% foreground
\begin{scope}[x={(\myxx,\myxy)},y={(\myyx,\myyy)},z={(\myzx,\myzy)},
canvas is xy plane at z=0,>=stealth]
\pgflowlevelsynccm
\draw[->] (0,-7) -- (0,-30);
\draw[ultra thick,red,->] (0,0) -- (-10,0);
\draw[thkline,->,overlay] (-50,0)+(-8:50) arc(-8:-20:50) node [above right] {$e^-$};
\end{scope}
\end{tikzpicture}
\end{document}
However, I was wondering if it might be possible to get the shape of that cone closer to the image above. In the end it's just a detail, but probably somebody here knows if and how that could be possible.
Thanks a lot in advance!

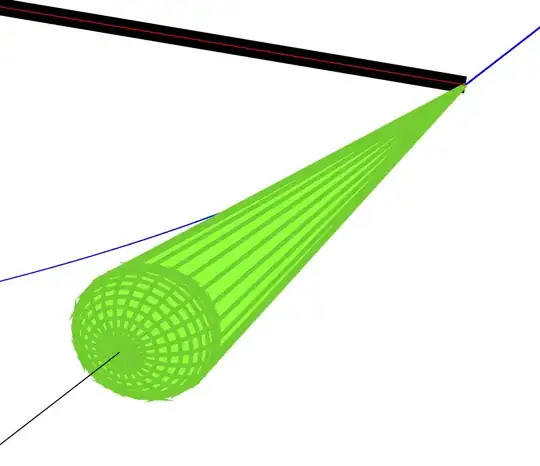
ifthenelseseems quite elegant. I wasn't aware of this option and learned something new, while having a beautiful solution - much appreciated! – Number42 Oct 29 '19 at 07:29