draw along a path in TikZ

Question

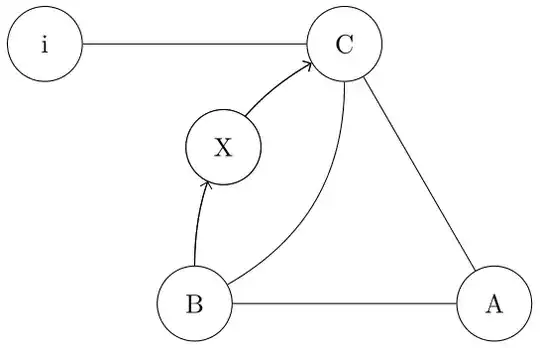
For the image and code below, how can I make the paths from B to X and from X to C fall exactly along the red path that's drawn from B to C?

I've managed to find the intersections of the red path and the node X, but I don't know how to find the angles into/out of X and C, and I don't know if setting something like tension would be needed even if I had the angles. Either doing something based on explicit calculations with the red path and node X or some more general / magic solution is fine.

Code:

\documentclass[margin=6]{standalone}

\usepackage{amsmath}

\usepackage{tikz}
\usetikzlibrary{positioning,calc}

\begin{document}

\begin{tikzpicture}[
  thick,
  every node/.style={
    draw,
    circle,
    minimum size=1cm,
  }
  ]
  \def\sep{4cm}
  \node (i) {i};
  \node at ($(i) + (0:\sep)$) (C) {C};
  \node at ($(C) + (-120:\sep)$) (B) {B};
  \node at ($(C) + (-60:\sep)$) (A) {A};

  \draw (i) -- (C);
  \draw (C) to [bend left] (B);

  \draw (B) -- (A);
  \draw (C) -- (A);

  % add a node
  \path [draw,red] (B) to [bend left] node [black,midway] (X) {X} (C);

  % but draw edges along the original (red) path
  \draw [->,shorten >=2pt] (B) to [bend left] (X);
  \draw [->,shorten >=2pt] (X) to [bend left] (C);

\end{tikzpicture}

\end{document}

Are arrows heads necessary for this path? other connection lines haven't them — Zarko, Oct 30 '19 at 17:22
It can be done with the methods of this answer. You can decompose the red path into intersection segments and then draw the relevant ones with the arrows attached. Please let me know if you need this to be spelled out. — , Oct 30 '19 at 17:27
@Schrödinger'scat That seems to work pretty well. The second last intersection segment \path [->,shorten >=2pt,draw,green,intersection segments={of=long arc and X circle,sequence={L-1}}]; seems to diverge slightly from the original path, but I guess I can live with it. — tsj, Oct 30 '19 at 18:08
Yes, these segments sometimes do not match absolutely perfectly, the reason being that at the basic level the curves are at most cubic Bézier curves. Glad to hear that it does work overall! — , Oct 30 '19 at 18:12

score 3 · Accepted Answer · answered Oct 30 '19 at 22:40

One way to draw your image is the following:

\documentclass[tikz, margin=6]{standalone}
\usetikzlibrary{arrows.meta,
                calc,
                intersections}

\begin{document}
    \begin{tikzpicture}[
                > = Straight Barb,
every node/.style = {circle, draw, minimum size=1cm}
                        ]
\def\sep{4cm}
  \node (i) {i};
  \node at ($(i) + (0:\sep)$) (C) {C};
  \node at ($(C) + (-120:\sep)$) (B) {B};
  \node at ($(C) + (-60:\sep)$) (A) {A};

  \draw (i) -- (C) 
        (C) to [bend left] (B) 
        (B) -- (A)
        (C) -- (A);
\draw[->, name path=bc]   
        (B) to [bend left] node [draw, fill=white, midway, name path=x] {X} (C);
\draw[->]   (B) to [bend left] node [draw, fill=white, midway] {X} (C);
\draw [name intersections={of=bc and x, by={x1,x2}},<-] 
    (x2) -- ++ (-105:0.01); % 105 = 120 - <band angle>/2
    \end{tikzpicture}
\end{document}

score 0 · Answer 2 · answered Oct 31 '19 at 01:11

It is possible to reconstruct the arcs without knowing the bending angle or adding things by hand. The arc is uniquely defined through three points on it, which can be taken the start point, p0, the end point p1, and the center of the node X. Given the center (and the radius) of the circle, it is absolutely straightforward to compute the angles of the point p0 and p1 as well as the intersections of the arc with the node boundary, i0 and i1. So you now the arc precisely, and can even bend the arrow heads appropriately.

\documentclass[margin=6]{standalone}
\usepackage{amsmath}
\usepackage{tikz}
\usetikzlibrary{positioning,calc,intersections,through,arrows.meta,bending}
\tikzset{circle through 3 points/.style n args={3}{% https://tex.stackexchange.com/a/461180
insert path={let    \p1=($(#1)!0.5!(#2)$),
                    \p2=($(#1)!0.5!(#3)$),
                    \p3=($(#1)!0.5!(#2)!1!-90:(#2)$),
                    \p4=($(#1)!0.5!(#3)!1!90:(#3)$),
                    \p5=(intersection of \p1--\p3 and \p2--\p4)
                    in },
at={(\p5)},
circle through= {(#1)}
}}
\begin{document}

\begin{tikzpicture}[
  thick,
  every node/.style={
    draw,
    circle,
    minimum size=1cm,
  }
  ]
  \def\sep{4cm}
  \node (i) {i};
  \node at ($(i) + (0:\sep)$) (C) {C};
  \node at ($(C) + (-120:\sep)$) (B) {B};
  \node at ($(C) + (-60:\sep)$) (A) {A};

  \draw (i) -- (C);
  \draw (C) to [bend left] (B);

  \draw (B) -- (A);
  \draw (C) -- (A);

  % add a node
  \path [%draw,red,
  name path=arc] (B) to [bend left] 
  node[black,midway,name path=X] (X) {X} 
  coordinate [pos=0] (p0) coordinate [pos=1] (p1)  (C);
  \node[circle through 3 points={p0}{X.center}{p1},overlay,draw=none](Y){};
  \path[name intersections={of=arc and X,by={i1,i0}}];
  \draw[-{Stealth[bend]}] let \p1=($(p0)-(Y.center)$),\p2=($(i0)-(Y.center)$),
   \n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)},\n3={veclen(\x1,\y1)} in
   (p0) arc(\n1:\n2-360:\n3);
  \draw[-{Stealth[bend]}] let \p1=($(i1)-(Y.center)$),\p2=($(p1)-(Y.center)$),
   \n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)},\n3={veclen(\x1,\y1)} in
   (i1) arc(\n1:\n2:\n3);
\end{tikzpicture}

\end{document}

draw along a path in TikZ

2 Answers2