Plot Dini's surface

Question

According to Wikipedia, the Dini's surface is described by the following parametric equations:

x = a \cos u \sin v
y = a \sin u \sin v
z = a (\cos v + \ln\tan v/2) + bu

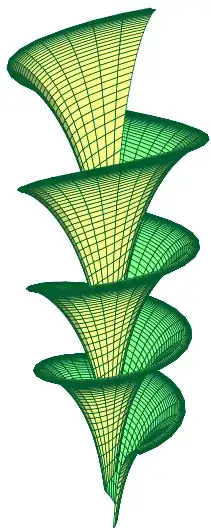
So, I'd like to plot the surface and obtain a result similar to the one below (got from here) to be used on a book cover (this is why I'd like to do it by myself instead of using the one from link):

I mean, the same shape, not necessarily the same coloring.

I tried the following code but far away from the result:

\documentclass{article}
\usepackage{pgfplots}

\begin{document}
\begin{tikzpicture}
 \begin{axis}[view={60}{30}]
  \addplot3[surf,shader=flat,
  samples=20,
  domain=0:14*pi,y domain=0:2,
  z buffer=sort]
  ({ 2 *cos(x) * sin(y)}, {2*sin(x) * sin(y)}, {2*(cos(y)+ln(tan(y/2))) + 0.15*x});
 \end{axis}
\end{tikzpicture}

\end{document}

Any idea how to reproduce the surface? It could be with different approach, not only pgfplots.

Edit: After using accepted solution below, I decided to edit here to show the result I got. Also, I searched for the colors in color map Pastel.

Code:

\documentclass[border=2mm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}

\begin{document}
\begin{tikzpicture}
  \begin{axis}[
    view={15}{10},
    hide axis,
    width=12cm,height=6cm,
    mesh/interior colormap=
      {pastel}{
      rgb255(0.00cm)=(194,120,239);
      rgb255(0.08cm)=(206,149,243);
      rgb255(0.17cm)=(220,165,196);
      rgb255(0.25cm)=(231,178,165);
      rgb255(0.33cm)=(238,194,152);
      rgb255(0.42cm)=(243,214,149);
      rgb255(0.50cm)=(245,232,151);
      rgb255(0.58cm)=(241,243,161);
      rgb255(0.67cm)=(227,240,185);
      rgb255(0.75cm)=(196,226,218);
      rgb255(0.83cm)=(151,204,243);
      rgb255(0.92cm)=(109,180,236);
      },
    colormap/cool,
    trig format plots=rad,
    point meta={z*z+y*y-0.3*z},
  ]
  \addplot3[
    surf,
    %shader=faceted,
    faceted color=black!80,
    %faceted color=mapped color!50,
    line width=0.1pt,
    samples=150, samples y=20,
    domain=1.5*pi:6.5*pi, y domain=0.02*pi:0.12*pi,
    z buffer=sort
  ]
  (
  {2*(cos(y)+ln(tan(y/2))) + 0.6*x},
  {2 *cos(x) * sin(y)},
  {-2*sin(x) * sin(y)} 
  );
  \end{axis}
\end{tikzpicture}
\end{document}

trig format plots=rad is a minor step in the right direction, I think. ;-) — , Nov 17 '19 at 00:01
@Schrödinger'scat, thanks. I never heard about it. Let me search for. — Sigur, Nov 17 '19 at 00:05
@Schrödinger'scat, and maybe some one knows the correct palette. Done. — Sigur, Nov 17 '19 at 03:06

score 24 · Accepted Answer · 2019-11-18T23:56:25.373

Wikipedia could be right. Most importantly, you need to add trig format plots=rad. Then you might reorder the axes directions, change the parameters and plot ranges, add different colormaps for the interior and outerior, add a point meta, and so on. This allows you to qualitatively reproduce their result.

\documentclass{article}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\begin{tikzpicture}
 \begin{axis}[view={10}{10},hide axis,
 width=12cm,height=6cm,
 colormap={bluegray}{color=(blue) color=(gray!20)},
 mesh/interior colormap={orangered}{color=(red) color=(orange)},
 trig format plots=rad,point meta={z*z+y*y-0.3*z}]
  \addplot3[surf,%shader=flat,
  samples=201,samples y=25,
  domain=1.5*pi:6.5*pi,y domain=0.02*pi:0.12*pi,
  z buffer=sort]
  ({2*(cos(y)+ln(tan(y/2))) + 0.6*x},{2 *cos(x) * sin(y)}, {-2*sin(x) * sin(y)} 
  );
 \end{axis}
\end{tikzpicture}
\end{document}

Or, if you want to see the trumpet shape more pronounced,

\documentclass{article}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\begin{tikzpicture}
 \begin{axis}[view={12}{10},hide axis,
 width=16cm,height=9cm,
 colormap={blueyellow}{color=(blue) color=(yellow)},
 mesh/interior colormap={orangeyellow}{color=(red) color=(yellow)},
 trig format plots=rad,point meta={z*z+y*y-0.5*z}]
  \addplot3[surf,%shader=flat,
  samples=101,samples y=15,
  domain=1.5*pi:6.5*pi,y domain=0.02*pi:0.48*pi,
  z buffer=sort]
  ({2*(cos(y)+ln(tan(y/2))) + 0.7*x},{2 *cos(x) * sin(y)}, {-2*sin(x) * sin(y)} 
  );
 \end{axis}
\end{tikzpicture}
\end{document}

Or with the color map Sigur.

\documentclass{article}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\begin{tikzpicture}
 \begin{axis}[view={12}{10},hide axis,
 width=16cm,height=9cm,
 colormap={Sigur inv}{rgb255(0cm)=(106,172,233); rgb255(1cm)=(241,238,141); rgb255(2cm)=(181,99,233)},
 mesh/interior colormap={Sigur}{rgb255(0cm)=(181,99,233); rgb255(1cm)=(241,238,141); rgb255(2cm)=(106,172,233)},
 trig format plots=rad,point meta={z*z+y*y-0.5*z}]
  \addplot3[surf,%shader=flat,
  samples=101,samples y=15,faceted color=blue!40!mapped color,
  domain=1.5*pi:6.5*pi,y domain=0.02*pi:0.48*pi,
  z buffer=sort,line width=0.01pt]
  ({2*(cos(y)+ln(tan(y/2))) + 0.7*x},{2 *cos(x) * sin(y)}, {-2*sin(x) * sin(y)} 
  );
 \end{axis}
\end{tikzpicture}
\end{document}

All of these can be animated in the usual way.

\documentclass[tikz,border=3mm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\foreach \X in {0,0.1,...,1.9}
{\begin{tikzpicture}
 \begin{axis}[view={12}{10},hide axis,
 width=16cm,height=9cm,
 colormap={Sigur inv}{rgb255(0cm)=(106,172,233); rgb255(1cm)=(241,238,141); rgb255(2cm)=(181,99,233)},
 mesh/interior colormap={Sigur}{rgb255(0cm)=(181,99,233); rgb255(1cm)=(241,238,141); rgb255(2cm)=(106,172,233)},
 trig format plots=rad,point meta={z*z+y*y-0.5*z}]
  \addplot3[surf,%shader=flat,
  samples=101,samples y=15,faceted color=blue!40!mapped color,
  domain={(1+\X)*pi}:{(6+\X)*pi},y domain=0.02*pi:0.48*pi,
  z buffer=sort,line width=0.01pt]
  ({2*(cos(y)+ln(tan(y/2))) + 0.7*x},{2 *cos(x) * sin(y)}, {-2*sin(x) * sin(y)} 
  );
 \end{axis}
\end{tikzpicture}}
\end{document}

I'll try to make it faster with more frames, and maybe smaller size to upload to the webpage. — Sigur, Nov 19 '19 at 00:35
@Sigur I think you should try mp3, see https://tex.stackexchange.com/a/462207/194703. The only reason I used gif here is that one cannot upload mp3 on this site. But if you have your own web site, mp3 might be better. The gif was created with convert -density 180 -delay 34 -loop 0 -alpha remove <file>.pdf ani.gif, see https://tex.stackexchange.com/a/136919/194703. — , Nov 19 '19 at 00:38
@Sigur You could ask for the code for the animation in the other answer and then compare performances.... ;-) (But such comparisons are never entirely fair, different codes have different numbers of plot points, different flexibility, and so on. With pgfplots you pay a price for being able to adjust the point meta at will, change the line colors along the path, and so on and so forth.) — , Nov 19 '19 at 00:47
I created a reversed gif with convert surface.gif -coalesce -duplicate 1,-2-1 -quiet -layers OptimizePlus -loop 0 ssurface.gif — Sigur, Nov 19 '19 at 00:49
@Sigur You could also do \foreach \X in {2,1.9,...,0.1} ... ;-) — , Nov 19 '19 at 00:50
@sigur, OK, you win. An mp3 can be played backwards, if I am not mistaken. — , Nov 19 '19 at 00:55

user187802 · Answer 2 · 2019-11-19T18:42:22.167

16

\listfiles
\documentclass[pstricks]{standalone}
\usepackage{pst-solides3d}
\begin{document}

\def\A{3.0}
\def\B{0.5}
\begin{pspicture}(-3.5,-3.5)(3.2,13)
\psset[pst-solides3d]{viewpoint=20 -20 30 rtp2xyz,Decran=15,lightsrc=viewpoint}
\defFunction[algebraic]{shell}(u,v)%
   {\A*cos(u)*sin(v)}%
   {\A*sin(u)*sin(v)}%
   {\A*(cos(v)+ln(tan(v/2))) + \B*u}
\psSolid[object=surfaceparametree, 
  linecolor={[cmyk]{1,0,1,0.5}}, 
  base=0 pi 8 mul  0.1 2, fillcolor=yellow!50,
  incolor=green!50, function=shell, linewidth=0.5\pslinewidth,ngrid=100 50]%
\end{pspicture}
\end{document}

\documentclass[pstricks]{standalone}
\usepackage{pst-solides3d}
\begin{document}

\def\A{3.0}
\def\B{0.5}
\multido{\iA=0+20}{18}{%
\begin{pspicture}(-3.5,-3.5)(3.2,13)
\psset[pst-solides3d]{viewpoint=20 \iA\space 30 rtp2xyz,Decran=15,lightsrc=viewpoint}
\defFunction[algebraic]{shell}(u,v)%
   {\A*cos(u)*sin(v)}%
   {\A*sin(u)*sin(v)}%
   {\A*(cos(v)+ln(tan(v/2))) + \B*u}
\psSolid[object=surfaceparametree, 
  linecolor={[cmyk]{1,0,1,0.5}}, 
  base=0 pi 8 mul  0.1 2, fillcolor=yellow!50,
  incolor=green!50, function=shell, linewidth=0.5\pslinewidth,ngrid=100 50]%
\end{pspicture}}
\end{document}

And then use convert from ImageMagick:

convert -delay 50 -loop 0 -density 300 -scale 300 -alpha remove test.pdf test.gif

The last animation has a fixed lightsource at 10 10 10

edited Nov 19 '19 at 18:42

answered Nov 17 '19 at 20:49

user187802

16,850

Beautiful color map. – Sigur Nov 17 '19 at 23:14
Please, could you post code for animation also? – Sigur Nov 19 '19 at 00:48
see edited answer – user187802 Nov 19 '19 at 07:10
Do you convert from dvi to pdf directly? Thanks so much. – Sigur Nov 19 '19 at 11:20
1

I am running xelatex, which uses xdvipdfmx in the background and the pdf is the default output format – user187802 Nov 19 '19 at 11:27
Do you know if it is possible to use some gradient in filling colors? – Sigur Nov 19 '19 at 12:05
I observed that the viewpoint are changing to give the movement illusion. How to make lightsrc constant? I mean, with the movement I'd like to see the shadow at same region like the light source was not moving. – Sigur Nov 19 '19 at 12:21
for example: lightsrc=10 10 10 rtp2xyz for a light source position at r=10, phi=10degrees, theta=10 degrees. Alternatively you can use `lightsrc=10 9 8' for x=10, y=9, x=8 – user187802 Nov 19 '19 at 14:24
What I'd like to obtain is: the source light at same position when creating another pages, that is, the light does not turn rotate witht he surface, so the shadow would be always as the same region of space. – Sigur Nov 20 '19 at 14:21
The first animation has a fixed region of the shadow. – user187802 Nov 20 '19 at 17:41
So, just use the 1st code within the animation code, right? Thanks a lot. – Sigur Nov 20 '19 at 18:51
yes, that's correct – user187802 Nov 20 '19 at 19:06

Plot Dini's surface

2 Answers2