tikz arithmetic with numbers and lengths

Question

Consider this example:

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
  \def\starty{3}
  \def\length{1};
  \coordinate(a1) at (1, \starty);
  \coordinate(b1) at ($(a1) + (0, -\length)$);
  \coordinate(a2) at (2, \starty - \length);
  \coordinate(b2) at ($(a2) + (0, \length)$);
  \draw[red, ->](a1) -- (b1);
  \draw[red, ->](b2) -- (a2);
  \draw (0, 0) -- (3, 0);
  \draw (0, 0) -- (0, 3);
\end{tikzpicture}
\end{document}

The result is 2 horizontally displaced arrows as it should be from a simple arithmetical inspection:

However, when I replace

  \def\length{1};

by

  \def\length{1cm};

the result is unexpected:

What is causing the discrepancy and how should I fix this example?

Answer 1

The issue is that you add/combine expressions with and without units. TikZ distinguishes between expressions with and without units. I recommend reading this answer. If you have

 \path (x,y) coordinate (p);

with x and y dimensionless, then the point p will be at x*(x unit vector)+y*(y unit vector). The initial values of these unit vectors are (1cm,0) and (0,1cm), respectively, but you can change them, e.g. with x=(1cm,0.2cm). (These changes are tricky if you do not supply units because if one uses x={({cos(20)},{(sin(20)})},y={({cos(20+90)},{(sin(20+90)})}, then one does not get just a rotated coordinate system. Rather, when y=... is parsed, it already uses the redefined x unit vector. This is why packages like tikz-3dplot attach units to define the rotated coordinate systems.)

If you have

 \path (x,y) coordinate (p);

where x and y carry units, then the point p will be at x to the right and y up (modulo transformations like rotations, of course). For the initial values of the unit vectors

 \path (1,2) coordinate (p);

and

 \path (1cm,2cm) coordinate (p);

yield the same results, but in general they don't. You can also have one coordinate with units and the other one without, e.g.

 \path (1cm,2) coordinate (p);

will lead to a point 1cm to the right and shifted by twice the y unit vector.

Now, coming to your question, if you present TikZ a mix

 \path (a+b,y) coordinate (p);

where a carries units and b does not, then TikZ will attach units pt to b. So, for instance, in

 \path (1cm+1,2) coordinate (p);

p will have an x coordinate of 1cm+1pt, while in

 \path (1+1,2) coordinate (p);

it will have an x coordinate of 2 times the x unit vector.

To illustrate this, I compare the coordinates of your MWE with those in which I appended pt to the dimensionless expressions, and show that they match.

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}

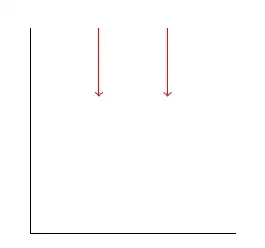
\subsection*{No units}

\begin{tikzpicture}
  \def\starty{3}
  \def\length{1};
  \coordinate(a1) at (1, \starty);
  \coordinate(b1) at ($(a1) + (0, -\length)$);
  \coordinate(a2) at (2, \starty - \length);
  \coordinate(b2) at ($(a2) + (0, \length)$);
  \draw[red, ->](a1) -- (b1);
  \draw[red, ->](b2) -- (a2);
  \draw (0, 0) -- (3, 0);
  \draw (0, 0) -- (0, 3);
\end{tikzpicture}

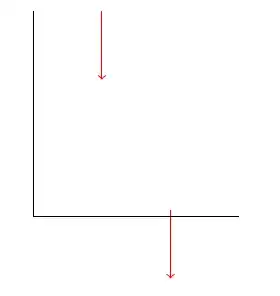
\subsection*{Mix of expressions with and without units}


\begin{tikzpicture}
  \def\starty{3}
  \def\length{1cm};
  \coordinate(a1) at (1, \starty);
  \coordinate(b1) at ($(a1) + (0, -\length)$);
  \coordinate(a2) at (2, \starty - \length);
  \coordinate(b2) at ($(a2) + (0, \length)$);
  \draw[red, ->](a1) -- (b1);
  \draw[red, ->](b2) -- (a2);
  \draw (0, 0) -- (3, 0);
  \draw (0, 0) -- (0, 3);
  \draw[<->,blue] (2,3pt-1cm) -- ++ (1,0) -- (2,3pt);
\end{tikzpicture}

\end{document}