UPDATE: A fully automatic solution. It keeps track of the numerators and denominators. The parser is very much inspired by the calc library of TikZ. \PrintFrac{<expression>} parses and simplifies the expression by dividing out greatest common divisor. The expression can contain integers, +, -, * and / (but no parentheses as of now).
\documentclass{article}
\usepackage{amsmath,amsfonts}
\usepackage[nice]{nicefrac}
\usepackage{pgf}
\usepgflibrary{fpu}
\makeatletter
%\def\mymessage#1{\message{#1^^J}}
\def\mymessage#1{}%
\pgfmathdeclarefunction{intfrac}{1}{%
\begingroup%
\edef\temp{\noexpand\pgfmathfracparse#1;}%
\temp%
\pgfmathsmuggle\pgfmathresult\endgroup%
}%
\long\def\pgfmathfracparse#1{%
\begingroup%
\def\pgf@frac@numerator{0}%
\def\pgf@frac@denominator{1}%
\def\pgf@current@frac@numerator{}%
\def\pgf@current@frac@denominator{}%
\def\pgf@local@frac@numerator{}%
\def\pgf@local@frac@denominator{1}%
\def\pgf@local@frac@above{1}%
\def\pgf@frac@factor{1}%
\def\pgf@local@frac@isprod{0}%
\def\pgf@prod@frac@numerator{1}%
\def\pgf@prod@frac@denominator{1}%
\pgf@frac@parse#1%
}%
\def\pgf@frac@parse{%
\pgfutil@ifnextchar;{%
% Ok, we found the end...
\pgf@frac@end%
}
{\pgfutil@ifnextchar+{%
% Ok, we found a term...
\pgf@frac@add%
}{%
\pgfutil@ifnextchar-{%
\pgf@frac@sub%
}{%
\pgfutil@ifnextchar/{%
\pgf@frac@div%
}{%
\pgfutil@ifnextchar *{%
\pgf@frac@prod%
}{% \tikzerror{+ or - or * or / expected}%
%\pgf@frac@end%
\pgf@frac@consume%
}%
}%
}%
}%
}%
}%
\def\pgf@frac@consume#1{%
\ifnum\pgf@local@frac@above=1
\edef\pgf@local@frac@numerator{\pgf@local@frac@numerator#1}%
\else
\edef\pgf@local@frac@denominator{\pgf@local@frac@denominator#1}%
\fi%
\mymessage{consuming #1 (numerator=\pgf@local@frac@numerator, denominator=\pgf@local@frac@denominator)^^J}%
\pgf@frac@parse%
}%
\def\pgf@frac@end;{%
%\mymessage{end\pgf@frac@numerator/\pgf@frac@denominator^^J}
%\def\pgf@local@frac@isprod{0}%
\pgf@frac@sumup%
\edef\pgfmathresult{\pgf@frac@numerator/\pgf@frac@denominator}%
\pgfmathsmuggle\pgfmathresult\endgroup}%
%
\def\pgf@frac@add+{%
\mymessage{saw a +^^J}%
\pgf@frac@sumup%
\def\pgf@frac@factor{1}%
\def\pgf@local@frac@isprod{0}%
\pgf@frac@parse%
}%
\def\pgf@frac@sub-{%
\mymessage{saw a -^^J}%
\pgf@frac@sumup%
\def\pgf@frac@factor{-1}%
\pgf@frac@parse%
}%
\def\pgf@frac@div/{%
\def\pgf@local@frac@above{0}%
\def\pgf@local@frac@denominator{}%
\pgf@frac@parse%
}%
\def\pgf@frac@prod *{%
\mymessage{* found^^J}%
\def\pgf@local@frac@above{1}%
%\mymessage{numerator was \pgf@prod@frac@numerator, denominator was \pgf@prod@frac@denominator^^J}%
\ifnum\pgf@local@frac@isprod=1
\pgfmathtruncatemacro{\pgf@prod@frac@numerator}{%
\pgf@prod@frac@numerator*\pgf@local@frac@numerator}%
\pgfmathtruncatemacro{\pgf@prod@frac@denominator}{%
\pgf@prod@frac@denominator*\pgf@local@frac@denominator}%
%\mymessage{numerator is \pgf@prod@frac@numerator, denominator is \pgf@local@frac@denominator^^J}%
\else
\def\pgf@local@frac@isprod{1}%
\pgfmathtruncatemacro{\pgf@prod@frac@numerator}{%
\pgf@local@frac@numerator}%
\pgfmathtruncatemacro{\pgf@prod@frac@denominator}{%
\pgf@local@frac@denominator}%
\fi
\def\pgf@local@frac@numerator{}%
\def\pgf@local@frac@denominator{1}%
\pgf@frac@consume%
}%
%
\def\pgf@frac@wrapupmul{%
\mymessage{wrap up *^^J}%
\mymessage{\pgf@prod@frac@numerator*\pgf@local@frac@numerator/\pgf@prod@frac@denominator*\pgf@local@frac@denominator^^J}%
\pgfmathtruncatemacro{\pgf@local@frac@numerator}{%
\pgf@prod@frac@numerator*\pgf@local@frac@numerator}%
\pgfmathtruncatemacro{\pgf@local@frac@denominator}{%
\pgf@prod@frac@denominator*\pgf@local@frac@denominator}%
\mymessage{now \pgf@local@frac@numerator/\pgf@local@frac@denominator^^J}%
\def\pgf@local@frac@isprod{0}%
}
\def\pgf@frac@sumup{%
\ifnum\pgf@local@frac@isprod=1
\pgf@frac@wrapupmul%
\fi
\ifnum\pgf@frac@factor<0
\mymessage{negative^^J}%
\fi
\pgfmathtruncatemacro{\pgf@current@frac@numerator}{%
\pgf@frac@factor*\pgf@frac@denominator*\pgf@local@frac@numerator+%
\pgf@frac@numerator*\pgf@local@frac@denominator}%
\mymessage{numerator:\pgf@frac@factor*\pgf@frac@denominator*\pgf@local@frac@numerator+%
\pgf@frac@numerator*\pgf@local@frac@denominator^^J}%
\pgfmathtruncatemacro{\pgf@current@frac@denominator}{%
\pgf@frac@denominator*\pgf@local@frac@denominator}%
\mymessage{denominator:\pgf@frac@denominator*\pgf@local@frac@denominator^^J}%
\mymessage{current numerator=\pgf@current@frac@numerator, current denominator=\pgf@current@frac@denominator^^J}%
%\mymessage{\pgf@frac@denominator*\pgf@local@frac@denominator^^J}%
\pgfmathtruncatemacro{\pgf@current@gcd}{gcd(\pgf@current@frac@denominator,%
\pgf@current@frac@numerator)}%
\pgfmathtruncatemacro{\pgf@frac@denominator}{\pgf@current@frac@denominator/\pgf@current@gcd}%
\pgfmathtruncatemacro{\pgf@frac@numerator}{\pgf@current@frac@numerator/\pgf@current@gcd}%
%\mymessage{fraction now:\pgf@frac@numerator/\pgf@frac@denominator^^J}%
\def\pgf@local@frac@above{1}%
\def\pgf@local@frac@numerator{}%
\def\pgf@local@frac@denominator{1}%
\def\pgf@local@frac@isprod{0}%
\def\pgf@prod@frac@numerator{1}%
\def\pgf@prod@frac@denominator{1}%
}%
\makeatother
\def \x {1/2}
\def \y {4/7}
\def \z {3}
\def \w {4}
\newcommand{\PrintFrac}[1]{\begingroup%
\def\pft##1/##2;{\def\mynum{##1}\def\myden{##2}}%
%\message{massaging #1^^J}%
\edef\temp{\noexpand\pgfmathsetmacro{\noexpand\ftest}{intfrac("#1")}}%
\temp%
\expandafter\pft\ftest;%
\ifnum\myden=1
\ensuremath{\mynum}%
\else
\ensuremath{\frac{\mynum}{\myden}}%
\fi
\endgroup}
\begin{document}
Consider the Matrix:
\[
\mathbb{A}=\left [
\begin{matrix}
\x & \y \\
\z & \w
\end{matrix}
\right ]
\]
Determinant should be calculated by:
\[
\det(\mathbb{A})=\PrintFrac{\x} \cdot \w -
(\PrintFrac{\y} \cdot \z)
= \PrintFrac{\x*\w} -
\PrintFrac{\y*\z} = \PrintFrac{\x*\w-\z*\y}
\]
\[\det(\mathbb{A})=\frac{1}{2} \cdot \w - (\frac{4}{7} \cdot \z) = 2 -\frac{12}{7} = \frac{2}{7}
\]
\PrintFrac{1/2+3*2/7-4*3/5}
\end{document}

This is not a completely automatic solution but it covers more cases. This is achieved by
- using
fpu for the computation,
- using
frac shift=2 as default, and
- adding an explicit
frac denom in more complicated cases.
These things are done with the \PrintFrac macro, which computes the fraction and does the above-mentioned things. It takes an optional argument, in which you can change the keys.
\documentclass{article}
\usepackage{amsmath,amsfonts}
\usepackage[nice]{nicefrac}
\usepackage{pgf}
\usepgflibrary{fpu}
\def \x {1/2}
\def \y {4/7}
\def \z {3}
\def \w {4}
\newcommand{\PgfmathsetmacroFPU}[2]{\begingroup% https://tex.stackexchange.com/a/503835
\pgfkeys{/pgf/fpu,/pgf/fpu/output format=fixed}%
\pgfmathsetmacro{#1}{#2}%
\pgfmathsmuggle#1\endgroup}%
\newcommand{\PrintFrac}[2][]{%
\PgfmathsetmacroFPU{\temp}{#2}%
\begingroup\pgfkeys{/pgf/number format/.cd,frac,frac whole=false,
/pgf/number format/frac shift=1,#1}%
\pgfmathprintnumber{\temp}\endgroup}
\begin{document}
\pgfkeys{/pgf/number format/.cd,frac, frac whole=false}%
Consider the Matrix:
\[
\mathbb{A}=\left [
\begin{matrix}
\x & \y \\
\z & \w
\end{matrix}
\right ]
\]
Determinant should be calculated by:
\[
\det(\mathbb{A})=\PrintFrac{\x} \cdot \w -
(\PrintFrac{\y} \cdot \z)
= \PrintFrac{\x*\w} -
\PrintFrac{\y*\z} = \PrintFrac[frac denom=7]{\x*\w-\z*\y}
\]
\end{document}

P.S. I do think that it should be possible to compute a parser that covers all cases.
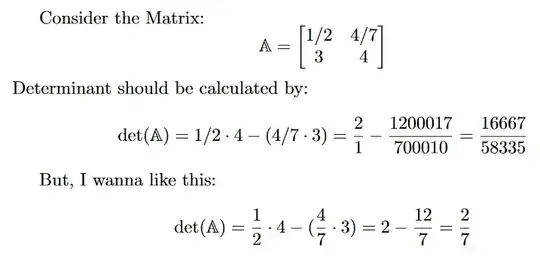


\PrintFrac{\x}and, if denom equals to 1 then write just only the integer associated, ie,2/1=2. What should I do? How may I putif...thento verify it? – fumachi Dec 06 '19 at 16:55\def \x {2}and\def \y {1/3}my code must result, forxthe value2, not2/1. The sum\x+\ymust be2+1/3=7/3. In this case,\PrintFrac[frac denom=7]{\x*\w-\z*\y}the result is a fraction, but could be just an integer. – fumachi Dec 06 '19 at 18:41