TikZ: Perpendicular line in a plane (3D problem)

Question

How to draw a line from the point X perpendicular to AB in the ground plane OAB?

Is there a simple mechanism or do I have to use something like tikz-3d?

\documentclass[margin=5pt, tikz]{standalone}
\usepackage{tikz}
\usetikzlibrary{calc}

\begin{document}
\pgfmathsetmacro{\a}{5}%  
\pgfmathsetmacro{\b}{5}%  
\begin{tikzpicture}[font=\footnotesize,]

\coordinate[label=left:$O$] (O) at (0,0,0); 
\coordinate[label=below:$B$] (B) at (\b,0,0); 
\coordinate[label=below:$A$] (A) at (0,0,\a); 
\coordinate[label=below:$X$] (X) at ($(A)!0.4!(B)$); 

\draw[] (A) -- (B);
\draw[help lines] (O) -- (A);
\draw[help lines] (O) -- (B);

\draw[red] (X) -- ($(X)!1 cm!-90:(A)$);


\begin{scope}[-latex, shift={(-0.5*\a,0.5*\a,0)}]
\foreach \P/\s/\Pos in {(1,0,0)/x/below, (0,1,0)/y/left, (0,0,2)/z/right} 
\draw[] (0,0,0) -- \P node[\Pos, pos=0.9,inner sep=2pt]{$\s$};
\end{scope}
\end{tikzpicture}
\end{document}

The main difference using tikz 3d is that the axes are equal in length. That is, if you rotate the image it doesn't appear to warp. — John Kormylo, Dec 13 '19 at 15:41

minhthien_2016 · Accepted Answer · 2021-11-03T09:12:31.780

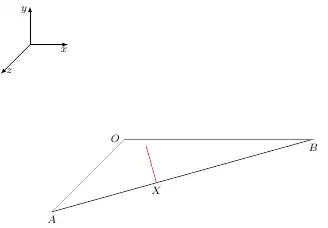
Let u = cross(OA,OB) and v = (B) - (A), then direction vector of the line that you want is found by cross(u,v). By calculating, we have cross(u,v)= {-a^2 b, 0, -a b^2}. I use {a,0,b} as direction vector of the line. Then I write the equation of the line through X and has direction vector, I get the point Y = (\b/4 -\a,0,3*\a/4-\b) on this line. The line though two points X and Y. I add the projection point H of the point O on the line AB. Note that, XY is parallel to OH.

\documentclass[margin=5pt, tikz]{standalone}
\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}
\pgfmathsetmacro{\a}{5}%

\pgfmathsetmacro{\b}{5}%

\begin{tikzpicture}[font=\footnotesize,]
\coordinate[label=left:$O$] (O) at (0,0,0); 
\coordinate[label=below:$B$] (B) at (\b,0,0); 
\coordinate[label=below:$A$] (A) at (0,0,\a); 
\coordinate[label=below:$X$] (X) at (\b/4,0,3\a/4); 
\coordinate[label=below:$Y$] (Y) at (\b/4 -\a,0,3\a/4-\b); 
\coordinate[label=below:$H$] (H) at ({\a\a\b/(\a\a+\b\b)}, 0, {\a\b\b/(\a\a+\b\b)});
\draw[] (A) -- (B);
\draw[help lines] (O) -- (A);
\draw[help lines] (O) -- (B);
\draw[red] (Y) -- (X) ;
\draw[blue] (O) -- (H) ;
\begin{scope}[-latex, shift={(-0.5\a,0.5\a,0)}]
\foreach \P/\s/\Pos in {(1,0,0)/x/below, (0,1,0)/y/left, (0,0,2)/z/right} 
\draw[] (0,0,0) -- \P node[\Pos, pos=0.9,inner sep=2pt]{$\s$};
\end{scope}
\end{tikzpicture}
\end{document}

enter image description here

In the above code, The coordinates of the point H is found by Maple soft. Based on this answer, you don't need find it.

    \documentclass[tikz,border=1 mm,12pt]{standalone}
\usepackage{fouriernc}
\usetikzlibrary{3dtools} 
\tikzset{intersection of line trough/.code args={#1 and #2 with plane
        containing #3 and normal #4}{%
        \pgfmathsetmacro{\ltest}{abs(TD("#2o#4")-TD("#1o#4"))}%
        \ifdim\ltest pt<0.01pt            
        \message{Plane and line are parallel!^^J}
        \pgfmathsetmacro{\myd}{0}
        \else
        \pgfmathsetmacro{\myd}{(TD("#3o#4")-TD("#1o#4"))/(TD("#2o#4")-TD("#1o#4"))}%
        \fi
        \pgfmathsetmacro{\myP}{TD("#1+\myd*#2-\myd*#1")}%
        \pgfkeysalso{insert path={%
                (\myP)
        }}
}}
\begin{document}
\pgfmathsetmacro{\a}{5}%

\pgfmathsetmacro{\b}{5}%

\begin{tikzpicture}
\path 
(0,0,0) coordinate (O)
 (\b,0,0) coordinate (B)
 (0,0,\a)  coordinate (A)
 ({\a\a\b/(\a\a+\b\b)}, 0, {\a\b\b/(\a\a+\b\b)}) coordinate (H')
 [
 3d coordinate={(myn)=(A)-(B)}
 ];
 \path[intersection of line trough={(A) and (B) with plane containing
    (O) and normal (myn)}] 
 coordinate (H);
 \foreach \p in {A,B,O,H}
 \draw[fill=black] (\p) circle (1.5pt);
 \foreach \p/\g in {A/135,B/90,O/180}
 \path (\p)+(\g:3mm) node{$\p$};
  \draw (A) -- (B) -- (O) -- cycle;
  \path[red] foreach \X in {H}
  {(\X) node[above] {$\X$} (\X') node[below] {$\X'$}};
  \draw (O) -- (H);
\end{tikzpicture}
\end{document}

With 3dtools

\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools,intersections,calc}
\begin{document}
\begin{tikzpicture}[3d/install view={phi=110,psi=0,theta=60},
    dot/.style={circle,inner sep=0pt,
        minimum size=2pt,fill}]
    \draw[every coordinate node/.append style={dot}]
    (2,1,2) coordinate[label=above:{$A$}] (A) --
    (1,2,1) coordinate[label=below:{$B$}] (B) --
    (2,0,0) coordinate[label=below:{$C$}] (C) -- cycle
    (0,0,0) coordinate[label=above:{$O$}] (O)
    (3,-2,1) coordinate[label=below:{$D$}] (D);
    \path[3d/plane through={(A) and (B) and (C) named pABC},
    3d/plane with normal={(1,1,1) through (C) named ptwo},
    3d/line through={(A) and (B) named lAB},
    3d/line through={(O) and (D) named lOD}];
    % project point on plane
    \path[3d/project={(O) on pABC}] coordinate (O');    
    % project point on line
    \path[3d/project={(C) on lAB}] coordinate (C');
    % intersection of plane and line
    \path[3d/intersection of={lOD with pABC}] coordinate (I);       
    \draw[dashed] (C) -- (C')
    coordinate[dot,label=above right:{$C'=\pgfmathparse{TD("(C')")}%
        (\pgfmathprintvector\pgfmathresult)^T$}];
    \path (O') coordinate[dot,label=right:{$O'=\pgfmathparse{TD("(O')")}%
        (\pgfmathprintvector\pgfmathresult)^T$}];
    \path (I) coordinate[dot,label=above:{$I=\pgfmathparse{TD("(I)")}%
        (\pgfmathprintvector\pgfmathresult)^T
        $}];
\end{tikzpicture}
\end{document}

Are you aware of the problems of /utils/exec? I see more and more people using it, because it was popularized by tallmarmot, but it doesn't actually work all that well. — Henri Menke, Dec 14 '19 at 06:05
@HenriMenke I copied the code at above link. I don't know it doesn't actually work all that well really. In this case, it works true. Thank you very much. — minhthien_2016, Dec 14 '19 at 06:11

Black Mild · Answer 2 · 2021-11-03T08:30:15.767

As @Henri Menke mentioned above, TikZ is not so suitable tool for orthogonal projection 3D.

For (3D) Asymptote, it is easy to get the foot of the perpendicular from a point P to segment AB using dot product as follows (it is straightforward from the definition of the dot product)

triple foot(triple P,triple A, triple B){ 
real s=dot(P-A,unit(B-A)); 
return A+s*unit(B-A);
}

So the code is natural!

// http://asymptote.ualberta.ca/
unitsize(1cm);
import three;
// The foot of the perpendicular from P to line AB:
triple foot(triple P,triple A, triple B){ 
real s=dot(P-A,unit(B-A)); 
return A+s*unit(B-A);
}
currentprojection=orthographic(2,1,1,zoom=.95,center=true);
triple A=(4,1,-1), B=(-2,5,1), C=(-1,-2.5,2);
triple H=foot(C,A,B);
draw(C--H,red+.8pt);
triple P=.8A+.2B;
triple Q=C+P-H;
draw(P--Q,blue+.8pt);
draw(surface(A--B--C--cycle),yellow+opacity(.8));
draw(A--B--C--cycle);
label("$A$",A,S);
label("$B$",B,E);
label("$C$",C,W);
label("$H$",H,SE);
label("$P$",P,SE);
label("$Q$",Q,W);
draw(Label("$x$",EndPoint),O--5X,Arrow3);
draw(Label("$y$",EndPoint),O--5Y,Arrow3);
draw(Label("$z$",EndPoint),O--4Z,Arrow3);
// to mark right angles
path3 Rmark(triple A, triple B, triple C, real size=.4){
triple Ba=B+sizeunit(A-B);
triple Bc=B+sizeunit(C-B);
triple Bt=Ba+Bc-B;
return Ba--Bt--Bc;

}
draw(Rmark(C,H,B),red);
draw(Rmark(Q,P,B,.5),blue);

You may want to check the perpendicularity.

TikZ: Perpendicular line in a plane (3D problem)

2 Answers2