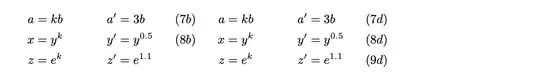The code below implements the equationgrid environment that allows the following syntax for these types of equations:
\begin{equationgrid}[Reference case, Modified Case]{one}%
a &= kb, a' &= 3b\\
x &= y^k, y' &= y^{0.5} \\
z &= e^k, z' &= e^{1.1}
\end{equationgrid}
The equations are numbered using the equation counter together with a "column" counter a, b, c, ... :

The equationgrid environment accepts two arguments:
- An optional header line that is a comma separated list of column headers.
- A required
label for the equations -- because I strongly believe that you should not label an equation unless you intend to refer to it later. In the example above, the subequations can be referred to using \ref{one-1a}, \ref{one-1b}, \ref{one-2a} and \ref{one-2b}.
Notice that the equations themselves are separated using commas, with \\ being used to mark the end of the equation line. The number of columns is, in principle, arbitrary. For example, you can use
\begin{equationgrid}{two}%
a &= kb, a' &= 3 b, a &= k b, a' &= 3 b\\
x &= y^k, y' &= y^{0.5}, x &= y^k, y' &= y^{0.5} \\
z &= e^k, z' &= e^{1.1}, z &= e^k, z' &= e^{1.1}
\end{equationgrid}
to produce

(The equation references for these equations are two-1a, two-1b, ..., two-3d.) These equations are typeset in an align* environment, so this environment and the page width limit how many columns can actually be used.
The code uses LaTex3 sequences in an essential way. First, the contents of the gridequation environment are split into rows using the newline separators \\ and then the rows are further split into columns using the commas. Once this is done the equations are reassembled with equation numbers and labels being added at the same time.
Here is the code:
\documentclass{article}
\usepackage{amsmath}
\usepackage{xparse}
% two counters for the keeping track of grid rows and columns
\newcounter{GridEqnCol}[equation]
\newcounter{GridEqnRow}
\renewcommand\theGridEqnCol{(\theequation\alph{GridEqnCol})}
\renewcommand\theGridEqnRow{\arabic{GridEqnRow}\alph{GridEqnCol}}
\ExplSyntaxOn
\int_new:N \l_grid_row_int % grid row number
\seq_new:N \l_grid_col_seq % the column entries in one row
\seq_new:N \l_grid_head_seq % the optional column headers
\seq_new:N \l_grid_row_seq % the rows of the equation
\tl_new:N \l_grid_hline_tl % a hack to adjust the columns
\tl_new:N \l_grid_label_tl % for construction equation labels
% \begin{equationgrid}[column headers as csv]{label}...\end{equationgrid}
\NewDocumentEnvironment{equationgrid}{ o m b }{
% split the environment body into rows using the \\
\tl_clear:N \l_grid_hline_tl
\int_zero:N \l_grid_row_int
\setcounter{GridEqnRow}{0}
\tl_set:Nn \l_grid_label_tl {#2-}
\seq_set_split:Nnn \l_grid_row_seq { \\ } { #3 }
\IfNoValueTF{#1}{ \seq_clear:N \l_grid_head_seq }
{
\seq_set_split:Nnn \l_grid_head_seq {,} {#1}
\tl_put_right:Nx \l_grid_hline_tl {
\noexpand\cline{1-\int_eval:n{2+4*\seq_count:N \l_grid_head_seq} }
}
}
\begin{align*}
\seq_if_empty:NF \l_grid_head_seq {
\seq_map_function:NN \l_grid_head_seq \__grid_head:n
\\\tl_use:N \l_grid_hline_tl
}
\seq_map_inline:Nn \l_grid_row_seq { \__grid_row:n {##1} }
\end{align*}
}{}
% typeset an entry of the header row
\cs_new:Npn \__grid_head:n #1 { \multispan{2}{\textbf{#1}} &&& }
% typeset an equation row, adding equation numbers and references
\cs_new:Npn \__grid_row:n #1 {
\refstepcounter{equation}
\refstepcounter{GridEqnRow}
% split #1 into column entries using the ,
\seq_set_split:Nnn \l_grid_col_seq { , } {#1}
\seq_map_inline:Nn \l_grid_col_seq {
\refstepcounter{GridEqnCol}
\tl_set:No \l_tmpa_tl {\tl_use:N \l_grid_label_tl \theGridEqnRow}
% align* disables equation numbers so need \ltx@label instead of \label
\use:c{ltx@label}{ \tl_use:N \l_tmpa_tl }
##1 & \theGridEqnCol &&
}
\\
}
\ExplSyntaxOff
\begin{document}
\begin{equationgrid}[Reference case, Modified Case]{one}%
a &= kb, a' &= 3b\\
x &= y^k, y' &= y^{0.5} \\
z &= e^k, z' &= e^{1.1}
\end{equationgrid}
\begin{equationgrid}{two}%
a &= kb, a' &= 3 b, a &= k b, a' &= 3 b\\
x &= y^k, y' &= y^{0.5}, x &= y^k, y' &= y^{0.5} \\
z &= e^k, z' &= e^{1.1}, z &= e^k, z' &= e^{1.1}
\end{equationgrid}
As you see, equations \ref{one-1a} and \ref{two-1a} are similar.
\end{document}
A final caveat: because the rows are separated by \\ and the columns by commas , you cannot use either of these inside the equations. If you want to insert commas then the easiest way would be use to \newcommand\comma{,}. I have followed the syntax of the OP but I would probably put a comma at the end of each equation.
EDIT
Here is an updated version of the code where the equationgrid environment now accepts an additional optional argument as <...> that gives a comma separated list of column indices for which the equation numbers should be omitted. In addition, you can place a \notag command in any cell to suppress the equation number for just that cell (note that the \notag command must be before the comma!). For example,
\begin{equationgrid}<1,3>{three}%
a &= kb, a' &= 3 b, a &= k b, a' &= 3 b\\
x &= y^k, y' &= y^{0.5}, x &= y^k, y' &= y^{0.5} \\
z &= e^k, z' &= e^{1.1}\notag, z &= e^k, z' &= e^{1.1}
\end{equationgrid}
suppresses the equation numbers in columns 1 and 3 and in row 3, column 2 to produce:
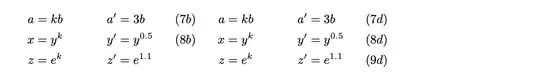
Here is the updated code:
\documentclass{article}
\usepackage{amsmath}
\usepackage{xparse}
% two counters for the keeping track of grid rows and columns
\newcounter{GridEqnCol}[equation]
\newcounter{GridEqnRow}
\renewcommand\theGridEqnCol{(\theequation\alph{GridEqnCol})}
\ExplSyntaxOn
\bool_new:N \g_print_eq_bool % suppress equation numbers in this column
\int_new:N \l_grid_row_int % grid row number
\seq_new:N \l_grid_col_seq % the column entries in one row
\seq_new:N \l_grid_head_seq % the optional column headers
\seq_new:N \l_grid_row_seq % the rows of the equation
\seq_new:N \l_suppress_eq_seq % suppress equation numbers in these columns
\tl_new:N \l_grid_hline_tl % a hack to adjust the columns
\tl_new:N \l_grid_label_tl % for construction equation labels
\renewcommand\theGridEqnRow{ \tl_use:N \l_grid_label_tl-\arabic{GridEqnRow}\alph{GridEqnCol} }
% \begin{equationgrid}<suppress column equation numbers>[column headers as csv]{label}...\end{equationgrid}
\NewDocumentEnvironment{equationgrid}{ D<>{} o m b }{
% split the environment body into rows using the \\
\tl_clear:N \l_grid_hline_tl
\int_zero:N \l_grid_row_int
\let\notag\relax % for completeness but not strictly necessary
\setcounter{GridEqnRow}{0}
\seq_set_split:Nnn \l_suppress_eq_seq { , } { #1 }
\tl_set:Nn \l_grid_label_tl {#3}
\seq_set_split:Nnn \l_grid_row_seq { \\ } { #4 }
\IfNoValueTF{#2}{ \seq_clear:N \l_grid_head_seq }
{
\seq_set_split:Nnn \l_grid_head_seq {,} {#2}
\tl_put_right:Nx \l_grid_hline_tl {
\noexpand\cline{1-\int_eval:n{2+4*\seq_count:N \l_grid_head_seq} }
}
}
\begin{align*}
\seq_if_empty:NF \l_grid_head_seq {
\seq_map_function:NN \l_grid_head_seq \__grid_head:n
\\\tl_use:N \l_grid_hline_tl
}
\seq_map_inline:Nn \l_grid_row_seq { \__grid_row:n {##1} }
\end{align*}
}{}
% typeset an entry of the header row
\cs_new:Npn \__grid_head:n #1 { \multispan{2}{\textbf{#1}} &&& }
% typeset an equation row, adding equation numbers and references
\cs_new:Npn \__grid_row:n #1 {
\refstepcounter{equation}
\refstepcounter{GridEqnRow}
% split #1 into column entries using the ,
\seq_set_split:Nnn \l_grid_col_seq { , } {#1}
\seq_map_inline:Nn \l_grid_col_seq {
\refstepcounter{GridEqnCol}
\bool_gset_true:N \g_print_eq_bool
\seq_if_in:NxT \l_suppress_eq_seq {\arabic{GridEqnCol}} { \bool_gset_false:N \g_print_eq_bool }
\str_if_in:nnT { ##1 } { \notag } { \bool_gset_false:N \g_print_eq_bool }
\bool_if:NT \g_print_eq_bool
{
% align* disables equation numbers so need \ltx@label instead of \label
\use:c{ltx@label}{ \theGridEqnRow }
}
##1 & \bool_if:NT \g_print_eq_bool {\theGridEqnCol} &&
}
\\
}
\cs_generate_variant:Nn \seq_if_in:NnF {NxF}
\ExplSyntaxOff
\begin{document}
\begin{equationgrid}[Reference case, Modified Case]{one}%
a &= kb, a' &= 3b\\
x &= y^k, y' &= y^{0.5} \\
z &= e^k, z' &= e^{1.1}
\end{equationgrid}
\begin{equationgrid}{two}%
a &= kb, a' &= 3 b, a &= k b, a' &= 3 b\\
x &= y^k, y' &= y^{0.5}, x &= y^k, y' &= y^{0.5} \\
z &= e^k, z' &= e^{1.1}, z &= e^k, z' &= e^{1.1}
\end{equationgrid}
As you see, equations \ref{one-1a} and \ref{two-1a} are similar.
\begin{equationgrid}<1,3>{three}%
a &= kb, a' &= 3 b, a &= k b, a' &= 3 b\\
x &= y^k, y' &= y^{0.5}, x &= y^k, y' &= y^{0.5} \\
z &= e^k, z' &= e^{1.1}\notag, z &= e^k, z' &= e^{1.1}
\end{equationgrid}
\end{document}