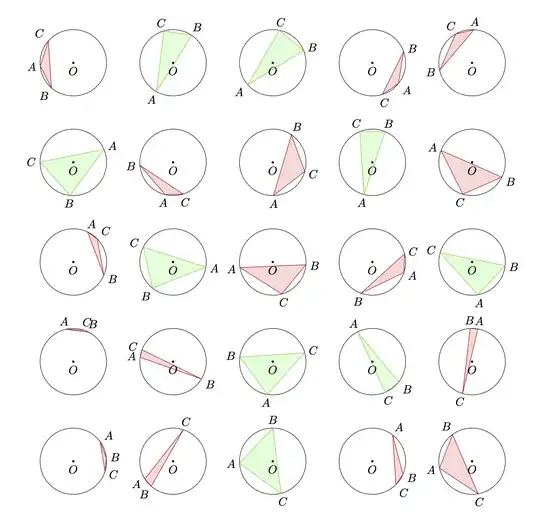
The problem I am modeling: Three points are randomly chosen on a circle. What is the probability that the triangle formed by these three points contains the center of the circle?
Conceptual understanding: Suppose we fix two of the three points, call them A and B. In order for the triangle to contain the center, the third point C must lie within the arc A'B', where A' and B' are the image of points A and B respectively under a rotation of 180 degrees.
What I want to happen: The randomly generated inscribed triangle to be filled green when it contains the center, and to fill red when it does not contain the center. I would also like to keep tally of the number of successes and failures to compute an experimental probability.
A few key things: I have access to the x and y coordinates of each point by using \pgfextractx and \pgfextracty. My method was to test whether the point C is between both the x-coordinates and y-coordinates of A and B by using \xintifboolexpr, however, this is flawed.
Minimal Working Example:
\documentclass{article}
\usepackage[left=2cm, right=2cm, top=2cm, bottom=1cm]{geometry}
\usepackage{amsmath,amsfonts,tikz,xintexpr,calc}
\newcommand\circletest{
\begin{tikzpicture}[scale=0.6]
\newdimen{\tempxa}
\newdimen{\tempya}
\newdimen{\tempxb}
\newdimen{\tempyb}
\newdimen{\tempxc}
\newdimen{\tempyc}
\def\radius{2}
\draw (0,0) coordinate (O);
\draw (O) circle[radius=\radius];
\draw (rnd*360:\radius) coordinate (A);
\pgfextractx\tempxa{\pgfpointanchor{A}{center}}
\pgfextracty\tempya{\pgfpointanchor{A}{center}}
\draw (rnd*360:\radius) coordinate (B);
\pgfextractx\tempxb{\pgfpointanchor{B}{center}}
\pgfextracty\tempyb{\pgfpointanchor{B}{center}}
\draw (rnd*360:\radius) coordinate (C);
\pgfextractx\tempxc{\pgfpointanchor{C}{center}}
\pgfextracty\tempyc{\pgfpointanchor{C}{center}}
\xintifboolexpr { (((\tempxc > -\tempxa) && (\tempxc < -\tempxb)) || ((\tempxc > -\tempxb) && (\tempxc < -\tempxa))) && (((\tempyc > -\tempya) && (\tempyc < -\tempyb)) || ((\tempyc > -\tempyb) && (\tempyc < -\tempya)))} %%I know this is grotesque
{\filldraw[color=green!80!black!100, fill=green!15] (A) -- (B) -- (C) -- cycle;} %true
{\filldraw[color=red!80!black!100, fill=red!15] (A) -- (B) -- (C) -- cycle;} %false
\fill[black] (A) circle[radius=2pt];
\fill[black] (B) circle[radius=2pt];
\fill[black] (C) circle[radius=2pt];
\fill[black] (O) circle[radius=2pt];
\draw (A) node[below]{A};
\draw (B) node[below]{B};
\draw (C) node[below]{C};
\end{tikzpicture}}
\begin{document}
\foreach \x in {0,1,...,11}{
\circletest
}
\end{document}
The issue I am having: Clearly my comparison operator \xintifboolexpr, along with my grotesque code following it is the problem. I am seeking a simpler method to tell if the point C is along the arc of the circle between (-\tempax,-\tempay) and (-\tempbx,-\tempby).
EDIT: A correct solution from Sandy G's suggestion.
\documentclass{article}
\usepackage[left=2cm, right=2cm, top=2cm, bottom=1cm]{geometry}
\usepackage{amsmath,amsfonts,tikz,xintexpr,calc}
\usepackage{xfp}
\newcommand\circletest{
\begin{tikzpicture}[scale=0.6]
\pgfmathsetmacro{\rndA}{rnd*360}
\pgfmathsetmacro{\rndB}{rnd*360}
\pgfmathsetmacro{\rndC}{rnd*360}
%defining x and y coordinates of each point
\def\radius{2}
\def\xa{\fpeval{\radius*cosd(\rndA)}}
\def\ya{\fpeval{\radius*sind(\rndA)}}
\def\xb{\fpeval{\radius*cosd(\rndB)}}
\def\yb{\fpeval{\radius*sind(\rndB)}}
\def\xc{\fpeval{\radius*cosd(\rndC)}}
\def\yc{\fpeval{\radius*sind(\rndC)}}
%calculating side lengths of triangle
\def\A{\fpeval{sqrt((\xb-\xc)^2 + (\yb-\yc)^2)}}
\def\B{\fpeval{sqrt((\xa-\xc)^2 + (\ya-\yc)^2)}}
\def\C{\fpeval{sqrt((\xa-\xb)^2 + (\ya-\yb)^2)}}
%calculating angles of triangle
\def\angleA{\fpeval{acosd((\B^2 + \C^2 -\A^2)/(2*\B*\C))}}
\def\angleB{\fpeval{acosd((\C^2 + \A^2 -\B^2)/(2*\C*\A))}}
\def\angleC{\fpeval{acosd((\A^2 + \B^2 -\C^2)/(2*\A*\B))}}
%defining some coordinates
\draw (0,0) coordinate (O);
\draw (O) circle[radius=\radius];
\draw (\xa,\ya) coordinate (A);
\draw (\xb,\yb) coordinate (B);
\draw (\xc,\yc) coordinate (C);
%test if center is in circle
\xintifboolexpr{((\angleA < 90) && (\angleB < 90)) && (\angleC < 90)}
{\filldraw[color=green!80!black!100, fill=green!15] (A) -- (B) -- (C) -- cycle;} %true
{\filldraw[color=red!80!black!100, fill=red!15] (A) -- (B) -- (C) -- cycle;} %false
%Drawing points on top of line
\draw[fill=black] (\xa,\ya) circle(1.5pt);
\draw[fill=black] (\xb,\yb) circle(1.5pt);
\draw[fill=black] (\xc,\yc) circle(1.5pt);
\draw[fill=black] (O) circle(1.5pt);
\end{tikzpicture}}
\begin{document}
\foreach \x in {0,1,...,30}{
\circletest
}
\end{document}