Coloured prism with TikZ

Question

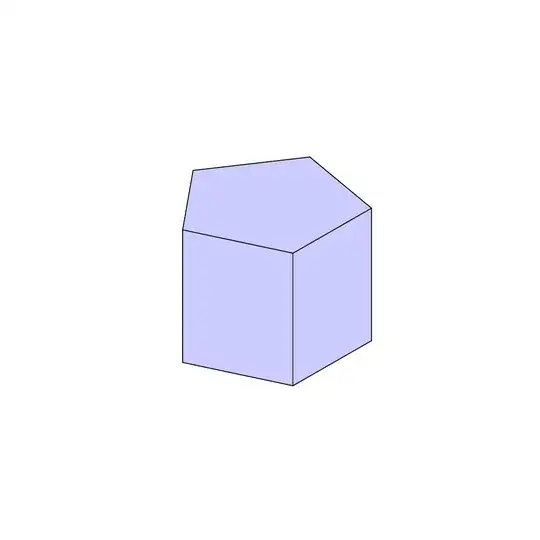
all.

I've drawn a pentagonal prism using TikZ's 3d library. Here's the code:

\documentclass[tikz,border=1cm]{standalone}
\colorlet{blu}{blue!10}
\usetikzlibrary{3d,
%   arrows
}

\begin{document}

\begin{tikzpicture}[opacity=0.8]
\newdimen\len
\len=2cm
%\foreach 
\begin{scope}[canvas is zx plane at y=0]
    \pgfmathsetmacro{\angle}{360/5}
    \draw[fill=blu] %
    (0:\len) coordinate (a0)
    \foreach \i in {1,...,4} {
        -- (\angle*\i:\len) coordinate (a\i) 
    } 
    -- cycle;
\end{scope}
\begin{scope}[canvas is zx plane at y=3]
\pgfmathsetmacro{\angle}{360/5}
\draw[fill=blu] %
(0:\len) coordinate (b0)
\foreach \i in {1,...,4} {
    -- (\angle*\i:\len) coordinate (b\i) 
} 
-- cycle;
\end{scope}
\draw (a3) -- (b3);
\draw[fill=blu] (a0) -- node [midway,anchor=north] {$l$} (a4) -- node[midway,anchor=east] {$h$} (b4) -- (b0);
\foreach \q in {0,1}{
    \pgfmathsetmacro{\s}{\q + 1}
    \draw[fill=blu] (a\s) -- (a\q) -- (b\q) -- (b\s) ;
}
\draw (a2) -- (b2);
\pgfmathsetmacro{\R}{5}
%\coordinate (O) at (0,0,0);
%\foreach \a/\pos in {x/north,y/east,z/west}
%   \draw[very thin,->] (O) -- (xyz cs: \a=\R) node[anchor=\pos] {$\a$};
\end{tikzpicture}

Although it works and it looks acceptable, I'd like to optimise this code using loops. Here's another MWE:

\documentclass[tikz,border=1cm]{standalone}
\colorlet{blu}{blue!10}
\usetikzlibrary{3d}

\begin{document}

\begin{tikzpicture}
\newdimen\len
\len=2cm
\foreach \i in {1,...,5} {
    \begin{scope}[canvas is xz plane at y=0] 
        \coordinate (a\i) at (\i*360/5:\len);
    \end{scope}
    \begin{scope}[canvas is xz plane at y=3]
        \coordinate (b\i) at (\i*360/5:\len);
    \end{scope}
    \draw (a\i) -- (b\i);
}
\foreach \q in {a,b}{
    \foreach \j in {1,...,4} {
        \pgfmathsetmacro\k{\j+1}
        \draw (\q\j) -- (\q\k);
    } 
    \draw (\q5) -- (\q1); %LOOP
}
\end{tikzpicture}

\end{document}

This works fine. What I don't know how to do now is how to fill it; I'd also very much like to Loop the drawing of the base pentagons (that's why I added the `%LOOP' comment). In the first example I commented the code for generating axes, but they are eventually going to appear in this figure. Having seen this post, I'd like to point out that I want the prism to be drawn like this, not with the pentagons as foreground and background (it's for a set of notes I'm writing and it is important that the prism be drawn like this).

I know one should ask one question per post, so what I'd really like to solve first is the filling part: how do I fill the faces of the second figure, drawn as it is?

Thanks!

Answer 1

I do not think that the 3d library gives you a great advantage here but here is an answer using it.

\documentclass[tikz,border=1cm]{standalone}
\colorlet{blu}{blue!10}
\usetikzlibrary{3d,backgrounds,perspective}

\begin{document}

\begin{tikzpicture}[3d view={65}{25}]
\newdimen\len
\len=2cm
\foreach \i in {1,...,6} {
    \begin{scope}[canvas is xy plane at z=0] 
        \coordinate (a\i) at (\i*360/5:\len);
    \end{scope}
    \begin{scope}[canvas is xy plane at z=3]
        \coordinate (b\i) at (\i*360/5:\len);
    \end{scope}
    \ifnum\i>1
    \draw[fill=blue!20,fill opacity=0.5]
      (b\the\numexpr\i-1) -- (a\the\numexpr\i-1) -- (a\i) -- (b\i) -- cycle;
    \fi
}
\begin{scope}[on background layer]
 \draw[fill=blue!20,fill opacity=0.5] plot[samples at={1,...,5}] (a\x);
\end{scope}
\draw[fill=blue!20,fill opacity=0.5] plot[samples at={1,...,5}] (b\x);
\end{tikzpicture}

\end{document}

As you can see, I could not resist and added an orthographic projection.

One way to make this fully rotatable is to employ this post, which requires the 3d tools library. (The development of this library is stalled because there seems to be no way to maintain it on GitHub.)

\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}
\begin{document}
\newcommand\GetProj[2]{\begingroup
\foreach \Coord [count=\nCoord] in #1
  {\ifnum\nCoord=1
  \xdef\temp{\Coord}
  \else
  \xdef\temp{\temp+\Coord}
  \fi}
  \edef\ntemp{\noexpand\path[overlay,3d coordinate={(tmp)=\temp}];}
  \ntemp
  \pgfmathsetmacro{#2}{TD("(n)o(tmp)")}
  \pgfmathsmuggle#2\endgroup}
\newcounter{tdorder}
\foreach \X in {1,...,20}
{\pgfdeclarelayer{layer\X}
\ifnum\X=1
\xdef\LstLayers{layer\X}
\else
\xdef\LstLayers{\LstLayers,layer\X}
\fi}
\pgfsetlayers\LstLayers
\tikzset{closed polygon/.style={insert path={foreach \Coord [count=\nCoord] in {#1}
 {\ifnum\nCoord=1
  \Coord
 \else
  -- \Coord
 \fi} -- cycle}},polygon/.style={insert path={foreach \Coord [count=\nCoord] in {#1}
 {\ifnum\nCoord=1
  \Coord
 \else
  -- \Coord
 \fi}}}}
%
\foreach \X in {5,15,...,355}
{\tdplotsetmaincoords{90-30*cos(\X)}{\X}
\begin{tikzpicture}[tdplot_main_coords,font=\sffamily,fill opacity=1]
  \path[tdplot_screen_coords,use as bounding box] (-5,-5) rectangle (5,5);
  \path foreach \X [count=\cX] in {b,t}
   {foreach \Y [count=\cY] in {A,B,C,D,E}
   {({2*cos(72*\cY)},{2*sin(72*\cY)},-4.5+3*\cX) coordinate(\X\Y)}};
  \def\PlaneData{%
  {draw,fill=blue!20}/closed polygon/{(bA),(tA),(tB),(bB)},%
  {draw,fill=blue!20}/closed polygon/{(bB),(tB),(tC),(bC)},%
  {draw,fill=blue!20}/closed polygon/{(bC),(tC),(tD),(bD)},%
  {draw,fill=blue!20}/closed polygon/{(bD),(tD),(tE),(bE)},%
  {draw,fill=blue!20}/closed polygon/{(bE),(tE),(tA),(bA)},%
  {draw,fill=blue!20}/closed polygon/{(tA),(tB),(tC),(tD),(tE)},%
  {draw,fill=blue!20}/closed polygon/{(bA),(bB),(bC),(bD),(bE)}}
  % normal of screen 
  \path[overlay] ({sin(\tdplotmaintheta)*sin(\tdplotmainphi)},
       {-1*sin(\tdplotmaintheta)*cos(\tdplotmainphi)},
       {cos(\tdplotmaintheta)}) coordinate (n); 
  % build up the list of projections       
  \foreach \Style/\Poly/\CoordLst [count=\nC] in \PlaneData
  {%
  \GetProj{\CoordLst}{\currproj}
  \ifnum\nC=1
    \xdef\LstProj{\currproj}
  \else
    \xdef\LstProj{\LstProj,\currproj}
  \fi}
  % draw the planes in appropriate layers
  \foreach \Style/\Poly/\CoordLst [count=\nC] in \PlaneData
  {%
  \GetProj{\CoordLst}{\currproj}
  \setcounter{tdorder}{1}
  \foreach \Proj in \LstProj
  {\pgfmathtruncatemacro{\itest}{ifthenelse(\Proj<\currproj,1,0)}
  \ifnum\itest=1
  \stepcounter{tdorder}
  \fi}
  \begin{pgfonlayer}{layer\number\value{tdorder}}
  \edef\temp{\noexpand\path[\Style,\Poly={\CoordLst}];}
  \temp
  \end{pgfonlayer}
  }
%   
\end{tikzpicture}}
\end{document}