Plot colormap of absolute value of a vector field with pgfplots

Question

Using matlab you can plot the absolute value of a vector field as a colormap to indicate the strength of the field at a given point. The result would look like this:

(Source code: https://scicomp.stackexchange.com/a/18774/11911)

Is it possible to do similar colormaps plots with pgfplots or another LaTeX plotting library? How to do it?

Edit

For answer just consider a simple example of a vector field like this:

\documentclass{article}
\usepackage{pgfplots}

\begin{document}

\begin{tikzpicture}
\begin{axis}[
xmin=-2,
xmax=2,
ymin=-2,
ymax=2,
view={0}{90}
]
\addplot3
[
samples=15,
->,
quiver={
  u={y},
  v={x},
  scale arrows=0.3,   
},
] {0};
%% Corresponding colormap is missing
\end{axis}
\end{tikzpicture}  
\end{document}

Well, yes, it is. However, you need some input like a vector field or some function that determines the vector field. Do you have an example? — , Apr 04 '20 at 22:03
I added an example. Which vector field to use doesn't matter in this question. — student, Apr 04 '20 at 22:17
However if someone reproduces the matlab picture with pgfplots including the varying arrow thickness, I consider to award 100 bounty points for that :-) — student, Apr 04 '20 at 22:23
The arrow thickness is easy to achieve: https://tex.stackexchange.com/a/134169. I guess the bigger problem might be to get function in, unless I misread the posts you link to they solve a differential equation numerically for that. — , Apr 04 '20 at 22:49

score 3 · Accepted Answer · 2020-04-04T23:02:16.547

How about this one? (Compiling with lualatex speeds up things considerably.)

\documentclass{article}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\pgfplotsset{/pgfplots/colormap={jet}{rgb255(0cm)=(0,0,128) rgb255(1cm)=(0,0,255)
rgb255(3cm)=(0,255,255) rgb255(5cm)=(255,255,0) rgb255(7cm)=(255,0,0)
rgb255(8cm)=(128,0,0)}}
\begin{document}
\begin{tikzpicture}
\begin{axis}[xmin=-2,xmax=2,ymin=-2,ymax=2,view={0}{90},
    colormap/jet]
\addplot3[surf,shader=interp,samples=101,point meta=-z]{min(sqrt(x*x+y*y),2.2)};
\addplot3
[samples=14,-stealth,quiver={u={y},v={x},scale arrows=0.3,}] {0};
\end{axis}
\end{tikzpicture}  
\end{document}

You can play with point meta max and point meta min, but I think the jet colormap is very close to what MatLab has. Together with this answer one can cook up e.g.

\documentclass{article}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\pgfplotsset{/pgfplots/colormap={jet}{rgb255(0cm)=(0,0,128) rgb255(1cm)=(0,0,255)
rgb255(3cm)=(0,255,255) rgb255(5cm)=(255,255,0) rgb255(7cm)=(255,0,0)
rgb255(8cm)=(128,0,0)}}
\begin{document}
\begin{tikzpicture}
\begin{axis}[xmin=-2,xmax=2,ymin=-2,ymax=2,view={0}{90},
    colormap/jet]
\addplot3[surf,shader=interp,samples=101,point meta=z]{2.2-min(sqrt(x*x+y*y),2.2)};
\addplot3[samples=24,
point meta={min(sqrt(x*x+y*y),2.2)},
quiver={u={y},v={x},scale arrows=0.18,
every arrow/.append style={%https://tex.stackexchange.com/a/134169
            line width=1.5pt*\pgfplotspointmetatransformed/1000,
            -stealth
        },
}] {0};
\end{axis}
\end{tikzpicture}  
\end{document}

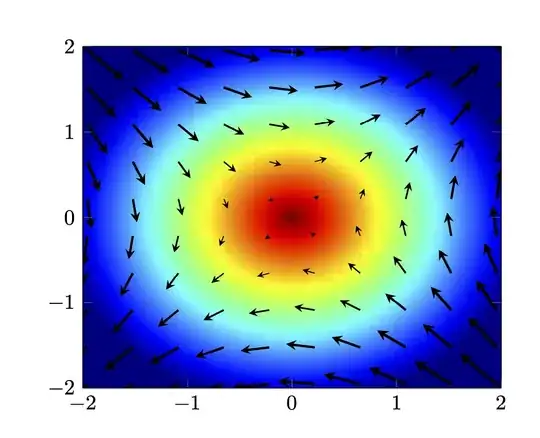
I think the main challenge for plotting "realistic" vector fields is not so much the presentation but solving the field equations to have some nice functions that can be fed in.

Plot colormap of absolute value of a vector field with pgfplots

1 Answers1