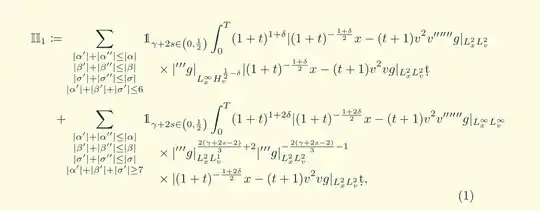1

So I was trying to improve the readability of my paper and was wondering if there is any way to make the following look slightly more appealing. enter image description here

Is it possible to have the sum sign with substack bigger and span over multiple math lines, some thing like enter image description here

For reference, the code I have is 

\begin{equation}\label{e.main_bound_Q2}
\begin{split}
\mathbb{II}_1:=\sum_{\substack{|\alpha'|+|\alpha''|\leq|\alpha|\\|\beta'|+|\beta''|\leq|\beta|\\|\sigma'|+|\sigma''|\leq|\sigma|\\|\alpha'|+|\beta'|+|\sigma'|\leq 6}}&\mathds{1}_{\gamma+2s\in \left(0,\frac{1}{2}\right)}\int_0^{T}(1+t)^{1+\delta}\norm{(1+t)^{-\frac{1+\delta}{2}}\jap{x-(t+1)v}^2\jap{v}\derv{''}{''}{''} g}_{L^2_xL^2_v}\\
&\times \norm{\derv{'}{'}{'} g}_{L^\infty_xH^{\frac{1}{2}-\delta}_v}\norm{(1+t)^{-\frac{1+\delta}{2}}\jap{x-(t+1)v}^2\jap{v}\der g}_{L^2_xL^2_v}\d t\\
\quad+\sum_{\substack{|\alpha'|+|\alpha''|\leq|\alpha|\\|\beta'|+|\beta''|\leq|\beta|\\|\sigma'|+|\sigma''|\leq|\sigma|\\|\alpha'|+|\beta'|+|\sigma'|\geq 7}}&\mathds{1}_{\gamma+2s\in \left(0,\frac{1}{2}\right)}\int_0^{T}(1+t)^{1+2\delta}\norm{(1+t)^{-\frac{1+2\delta}{2}}\jap{x-(t+1)v}^2\jap{v}\derv{''}{''}{''} g}_{L^\infty_xL^{\infty}_v}\\
&\qquad\times \norm{\derv{'}{'}{'} g}_{L^2_xL^1_v}^{\frac{2(\gamma+2s-2)}{3}+2}\norm{\derv{'}{'}{'} g}_{L^2_xL^2_v}^{-\frac{2(\gamma+2s-2)}{3}-1}\\
&\qquad\times \norm{(1+t)^{-\frac{1+2\delta}{2}}\jap{x-(t+1)v}^2\jap{v}\der g}_{L^2_xL^2_v}\d t,
\end{split}
\end{equation}
Leucippus
  • 1,636
Sanchit
  • 13
  • 2
  • You might consider adding something vaguely along the lines of "We denote the system of inequalities [your first three inequalities] by [some brief X]", and then substituting that in for a less awkward substack.. – Fintan May 12 '20 at 02:38

3 Answers3

3

I agree with @Fintan's comment that it is a good idea to define a variable to denote the inequalities. But if you want to use a substack, one option is to simply \smash the sum: (I didn't bother with defining all the missing macros to create a MWE):

\documentclass{article}
\usepackage{mathtools, amsfonts, dsfont}
\DeclarePairedDelimiter\norm{\lvert}{\rvert}
\let\jap\relax
\let\derv\relax
\let\der\relax


\begin{document}
\begin{equation} \begin{split}
    \label{e.main_bound_Q2}
    \mathbb{II}_1 \coloneqq 
      \smash{\sum_
        {\substack{|\alpha'|+|\alpha''|\leq|\alpha| \\
                   |\beta'|+|\beta''|\leq|\beta|\\|\sigma'|+|\sigma''|\leq|\sigma|\\
                   |\alpha'|+|\beta'|+|\sigma'|\leq 6}}}
      &\mathds{1}_{\gamma+2s\in \left(0,\frac{1}{2}\right)}
      \int_0^{T}(1+t)^{1+\delta}
      \norm{(1+t)^{-\frac{1+\delta}{2}}
      \jap{x-(t+1)v}^2\jap{v}
      \derv{''}{''}{''} g}_{L^2_xL^2_v}
    \\
    &\quad\times 
      \norm{\derv{'}{'}{'} g}_{L^\infty_xH^{\frac{1}{2}-\delta}_v}
      \norm{(1+t)^{-\frac{1+\delta}{2}}
      \jap{x-(t+1)v}^2
      \jap{v}\der g}_{L^2_xL^2_v}\d t
    \\[10pt]
    \quad+
    \smash{\sum_
        {\substack{|\alpha'|+|\alpha''|\leq|\alpha|\\
                   |\beta'|+|\beta''|\leq|\beta|\\|\sigma'|+|\sigma''|\leq|\sigma|\\
                   |\alpha'|+|\beta'|+|\sigma'|\geq 7}}}
    &\mathds{1}_{\gamma+2s\in \left(0,\frac{1}{2}\right)}
     \int_0^{T}(1+t)^{1+2\delta}
     \norm{(1+t)^{-\frac{1+2\delta}{2}}
     \jap{x-(t+1)v}^2\jap{v}
     \derv{''}{''}{''} g}_{L^\infty_xL^{\infty}_v}
    \\
    &\quad\times 
     \norm{\derv{'}{'}{'} g}_{L^2_xL^1_v}^{\frac{2(\gamma+2s-2)}{3}+2}
     \norm{\derv{'}{'}{'} g}_{L^2_xL^2_v}^{-\frac{2(\gamma+2s-2)}{3}-1}
    \\
    &\quad\times
      \norm{(1+t)^{-\frac{1+2\delta}{2}}
      \jap{x-(t+1)v}^2
      \jap{v}\der g}_{L^2_xL^2_v}\d t,
  \end{split}
\end{equation}
\end{document}

which gives

enter image description here

Aditya
  • 62,301
  • Thanks for the answer. This is quite nice. The issue with defining the inequalities with a new variable is that I have 14 terms like this haha – Sanchit May 12 '20 at 19:31
1

A poor implementation of \xmathlarger[<larger size>]{<equation>}, based on \larger from relsize package.

The name of command \xmathlarger follows \mathlarger from relsize package, see this answer for a use example for \mathlarger.

\documentclass{article}
\usepackage{amsmath}
\usepackage{relsize}

\makeatletter
\newcommand\xmathlarger[2][1]{%
  \mbox{\larger[#1]$\displaystyle#2\m@th$}%
}
\makeatother

\begin{document}
Normal size
\[
  \sum a + b
\]

Enlarged size
\[
  \mathop{\xmathlarger[3]{\sum}}_{\substack{i = 1 \\ j = 1}}
  \begin{aligned}
    a &+ b \\
      &+ c + d
  \end{aligned}
\]
\end{document}

enter image description here

muzimuzhi Z
  • 26,474
1

You might use nested aligned. I'd exclude enlarging the summation sign.

I supplied mock definitions for \derv and \der. About \d, I'd not encourage using \renewcommand on it; when your bibliography will contain some author where \d (underdot accent) is needed, you'll be in big trouble.

\documentclass{article}
\usepackage{amsmath,mathtools,amssymb,dsfont}

\DeclarePairedDelimiter{\norm}{\lVert}{\rVert}
\DeclarePairedDelimiter{\jap}{\langle}{\rangle}

\newcommand{\derv}[3]{DERV}%????
\newcommand{\der}[1]{#1}%   ????
\newcommand{\diff}{\mathop{}\!\mathrm{d}}

\begin{document}

\begin{equation}\label{e.main_bound_Q2}
\begin{split}
\mathbb{II}_1:=
\sum_{\substack{
  |\alpha'|+|\alpha''|\leq|\alpha|\\
  |\beta'|+|\beta''|\leq|\beta|\\
  |\sigma'|+|\sigma''|\leq|\sigma|\\
  |\alpha'|+|\beta'|+|\sigma'|\leq 6
}}&
\begin{aligned}[t]
 &\mathds{1}_{\gamma+2s\in \left(0,\frac{1}{2}\right)}
  \int_0^{T}(1+t)^{1+\delta}\norm{(1+t)^{-\frac{1+\delta}{2}}\jap{x-(t+1)v}^2\jap{v}
  \derv{''}{''}{''} g}_{L^2_xL^2_v}\\
 &\qquad\times \norm{\derv{'}{'}{'} g}_{L^\infty_xH^{\frac{1}{2}-\delta}_v}
         \norm{(1+t)^{-\frac{1+\delta}{2}}\jap{x-(t+1)v}^2\jap{v}\der g}_{L^2_xL^2_v}\diff t
\end{aligned}
\\[2ex]
+\sum_{\substack{
  |\alpha'|+|\alpha''|\leq|\alpha|\\
  |\beta'|+|\beta''|\leq|\beta|\\
  |\sigma'|+|\sigma''|\leq|\sigma|\\
  |\alpha'|+|\beta'|+|\sigma'|\geq 7
}}&
\begin{aligned}[t]
 &\mathds{1}_{\gamma+2s\in \left(0,\frac{1}{2}\right)}
  \int_0^{T}(1+t)^{1+2\delta}\norm{(1+t)^{-\frac{1+2\delta}{2}}\jap{x-(t+1)v}^2
  \jap{v}\derv{''}{''}{''} g}_{L^\infty_xL^{\infty}_v}\\
 &\qquad\times \norm{\derv{'}{'}{'} g}_{L^2_xL^1_v}^{\frac{2(\gamma+2s-2)}{3}+2}
  \norm{\derv{'}{'}{'} g}_{L^2_xL^2_v}^{-\frac{2(\gamma+2s-2)}{3}-1}\\
 &\qquad\times \norm{(1+t)^{-\frac{1+2\delta}{2}}\jap{x-(t+1)v}^2\jap{v}\der g}_{L^2_xL^2_v}\diff t,
\end{aligned}
\end{split}
\end{equation}

\end{document}

enter image description here

egreg
  • 1,121,712