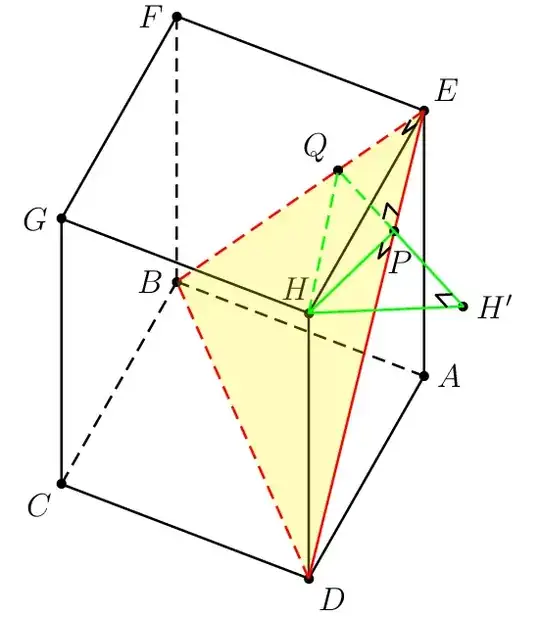
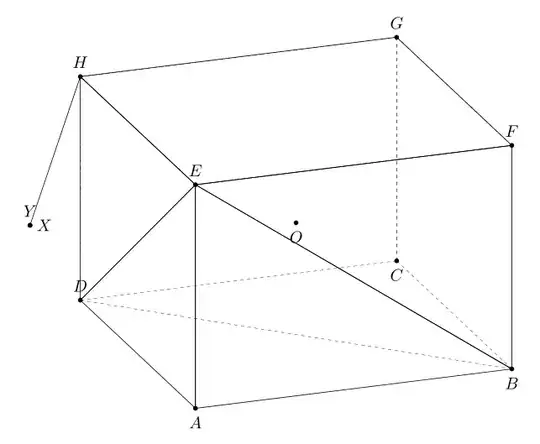
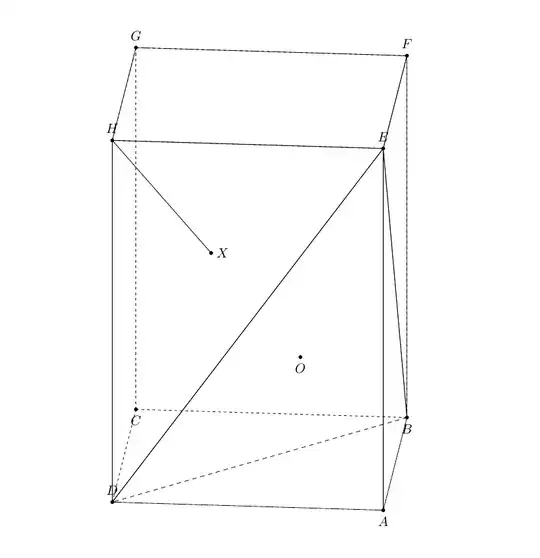
First consider the following example for illustration purposes. The objective is to draw the shortest line segment from the point H to the plane BDE. The prism ABCD.EFGH has AB=AD=5\sqrt{2} and AE=12. I think that these numbers are badly selected by the author.
The following is my attempt to draw it with pst-3dplot (with premature 3D support) and pst-eucl (designed only fo 2D). The process is tedious because many tasks such as
- defining a new 3D colinear point from 2 existing 3D points with a certain scaling factor,
- projecting an existing 3D point onto a line joining two existing 3D points,
- marking right angle with a slanted perpendicular symbol,
are performed with manual calculation beforehand. Among others, \pstProjection and \pstRightAngle from pst-eucl do not work in 3D.
Here it is the painful parts that I did. Look at the magic exact numbers.
\pstHomO[HomCoef=\pscalculate{50/194},PosAngle=-80]{E}{D}[P]
\pstHomO[HomCoef=\pscalculate{25/72},PosAngle=135]{E}{B}[Q]
\pstHomO[HomCoef=\pscalculate{9409/4225},PosAngle=0]{Q}{P}[H']
Other operations such as
- projecting an existing 3D point onto a plane passing through 3 existing 3D points,
- finding the intersecting point between two lines, each passing through 2 distinct points,
- etc
are also required in the future projects.
Question
Here I want to know which LaTeX packages really support 3D drawing operation above with ease. Redrawing what I did below to prove the effectiveness of package you propose is required. I don't know much about Asymptote, TikZ, Metapost, and others.
My painful attempt
\documentclass[pstricks,border=0cm,12pt]{standalone}
\usepackage{pst-3dplot,pst-eucl}
\psset{unit=5mm}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% OBJECTIVE
% Draw the shortest line segment
% from the point H to
% the plane BDE .
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\def\pstSlantedRightAngle#1#2#3{%
\pnodes([nodesep=6pt]{#1}#2){s}([nodesep=6pt]{#3}#2){t}
\pstTranslation[PointName=none,PointSymbol=none]{#2}{s}{t}[u]
\psline(s)(u)(t)}
\begin{document}
\begin{pspicture}showgrid=false(6,15)
\psset{Alpha=-115,Beta=55}
% prism ABCD.EFGH
\def\A{(5 2 sqrt mul,0,0)}
\def\B{(5 2 sqrt mul,5 2 sqrt mul,0)}
\def\C{(0,5 2 sqrt mul,0)}
\def\D{(0,0,0)}
\def\E{(5 2 sqrt mul,0,12)}
\def\F{(5 2 sqrt mul,5 2 sqrt mul,12)}
\def\G{(0,5 2 sqrt mul,12)}
\def\H{(0,0,12)}
% hidden lines do not work!
%\edef\coor{\D\A\C\H}
%\expandafter\pstThreeDBox\coor
\foreach \i in {A,B,...,H}{%
\edef\coor{\csname\i\endcsname}
\expandafter\pstThreeDDot\coor
\expandafter\pstThreeDNode\coor{\i}
}
\foreach \i/\j in {0/A,180/B,-135/C,-45/D,45/E,180/F,180/G,115/H}{\uput[\i](\j){$\j$}}
\pspolygon(C)(D)(A)(E)(F)(G)
\psline(H)(E)
\psline(H)(G)
\psline(H)(D)
\psline[linestyle=dashed](B)(F)
\psline[linestyle=dashed](B)(C)
\psline[linestyle=dashed](B)(A)
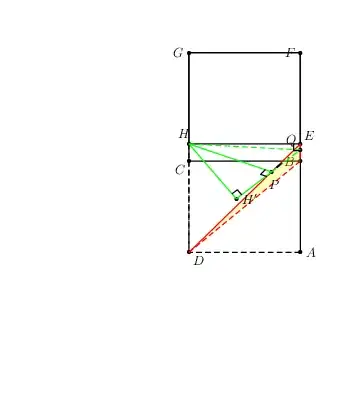
% plane EDB
\pspolygon[fillstyle=solid,fillcolor=yellow,opacity=0.25,linestyle=none,linewidth=0](E)(B)(D)
\psline[linestyle=dashed,linecolor=red](E)(B)(D)
\psline[linecolor=red](E)(D)
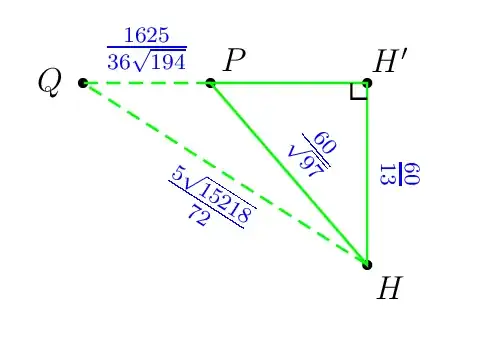
% the shortest distance from H to EDB
\pstHomO[HomCoef=\pscalculate{50/194},PosAngle=-80]{E}{D}[P]
\pstHomO[HomCoef=\pscalculate{25/72},PosAngle=135]{E}{B}[Q]
\pstHomO[HomCoef=\pscalculate{9409/4225},PosAngle=0]{Q}{P}[H']
\psline[linestyle=dashed,linecolor=green](H)(Q)(P)
\pspolygon[linecolor=green](P)(H')(H)
% right-angle mark
\pstSlantedRightAngle{H}{P}{D}
\pstSlantedRightAngle{E}{P}{Q}
\pstSlantedRightAngle{H}{H'}{P}
\pstSlantedRightAngle{H}{E}{Q}
\end{pspicture}
\end{document}
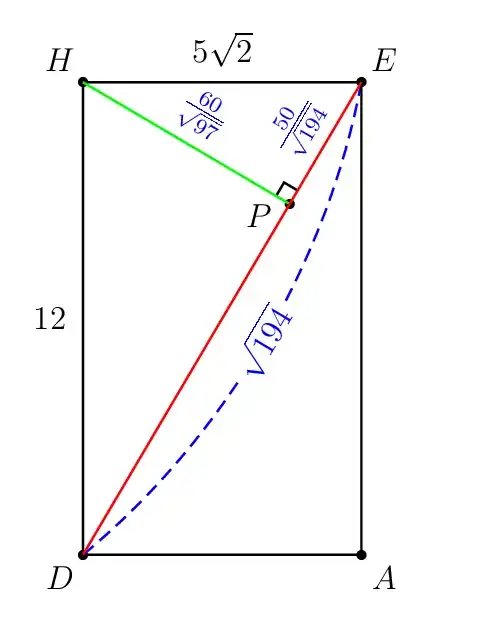
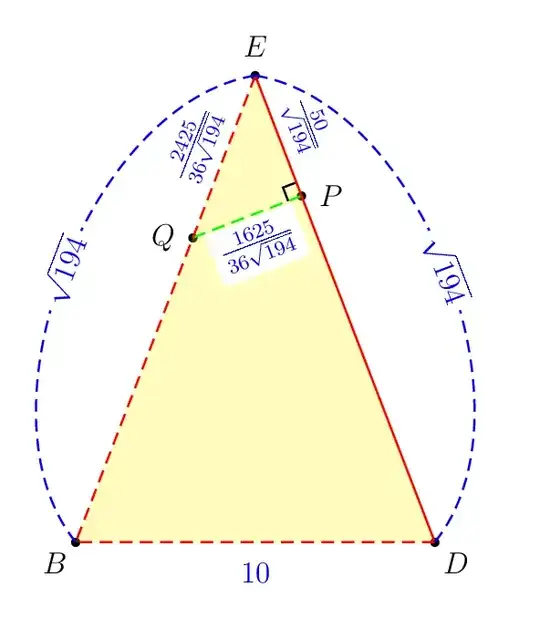
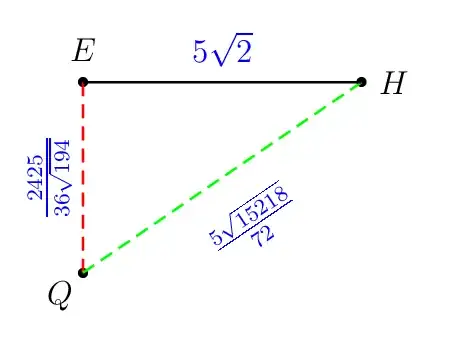
Behind the scene calculation
I love Euclidean geometry!
In some cases, the hidden lines are wrongly rendered!



I don't know much about Asymptote, TikZ, Metapost, and others.Hmm, you can refresh your brain and start with one of them! :-) – Jun 17 '20 at 12:19Hto the plane(DBE)is60/13. – minhthien_2016 Feb 13 '21 at 15:12a = 5*sqrt(2) and h = 12, then projection of the pointHon the plane(DBE)is({a*h*h/(a*a+2*h*h)}, {-a*h*h/(a*a+2*h*h)}, {2*h*h*h/(a*a+2*h*h)})– minhthien_2016 Feb 13 '21 at 15:44skeletonin connection withP=currenprojection(see http://asy.marris.fr/asymptote/Solides/index.html). For complicated 3D figure, there is no cheap and general method. – Black Mild Feb 21 '21 at 04:22P=currenprojection? If yes, I will invest my time to master asymptote. :-) – Display Name Feb 22 '21 at 03:24