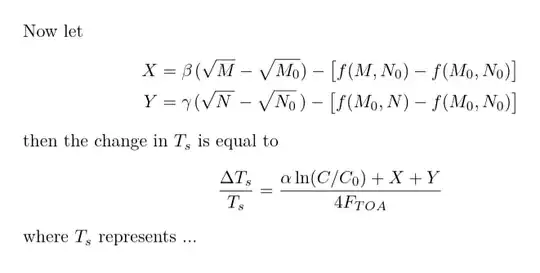LaTex error : "Missing } inserted"

Question

I have written this :

\begin{multline}
\Delta T_s = \frac{T_s \times (\alpha \ln \frac{C}{C_0} + (\beta(\sqrt{M} - \sqrt{M_0})\\
- (f(M, N_0) - f(M_0, N_0))) + (\gamma (\sqrt{N} - \sqrt{N_0}) - (f(M_0, N) - f(M_0, N_0)))}{4F_{TOA}}
\end{multline}

but latex gives me the error "Missing } inserted", i tried some stuff but everytime latex gives me this. Can you help me please ?

Answer 1

The immediate reason for the error is the fact that you've inserted \\ in the numerator term of the \frac directive. I have removed it and it is works correctly.

\documentclass[a4paper,12pt]{article}
\usepackage{amsmath}
\begin{document}
\begin{multline}
\Delta T_s = \frac{T_s \times (\alpha \ln \frac{C}{C_0} + (\beta(\sqrt{M} - \sqrt{M_0})
- (f(M, N_0) - f(M_0, N_0))) + (\gamma (\sqrt{N} - \sqrt{N_0}) - (f(M_0, N) - f(M_0, N_0)))}{4F_{TOA}}
\end{multline}
\end{document}

---

To create a line break in the numerator, you can use \splitfrac, a macro provided by the mathtools package.

\documentclass{article}
\usepackage{mathtools}
\begin{document}
\begin{equation}
\Delta T_s =\frac{\splitfrac{T_s \times [\alpha \ln \frac{C}{C_0} + (\beta(\sqrt{M} - \sqrt{M_0},)

(f(M, N_0) - f(M_0, N_0))] }{+\gamma (\sqrt{N} - \sqrt{N_0},) - (f(M_0, N) - f(M_0, N_0))}}{4F_{\mathit{TOA}}}

\end{equation}
\end{document}

Answer 2

I think you should use the \splitfrac from mathtools to make this long fraction fit textwidth. I also used different sizes for parentheses tm make the fraction more readable:

\documentclass[a4paper,12pt]{article}
\usepackage{mathtools}
\begin{document}
\[ \Delta T_s = \frac{\splitfrac{T_s \times\Bigl(\alpha \ln \frac{C}{C_0} + \beta\bigl(\sqrt{M} - \sqrt{M_0}\bigr)


\bigl(f(M, N_0) - f(M_0, N_0)\bigr)\Bigr)}{+ \Bigl(\gamma \bigl(\sqrt{N} - \sqrt{N_0}\bigr) - \bigl(f(M_0, N) - f(M_0, N_0)\bigr)\Bigr)}}{4F_{TOA}} ]%

\end{document} 

Answer 3

I know this is an old question, and I do not want to necro-bump it. However, I feel like the given answers somewhat misses the point. Yes, if you have to keep everything in a single equation, multiline is the way to go. But do you really have to? I can only think of a few circumstances.

• I am submitting to a journal and I am really tight on space
• I am working on a two or three?! column document and are tight on space.

---

In any other circumstance I would recommend rewriting the surrounding text, which will make it more bearable for the reader to digest as well. One suggestion could look like

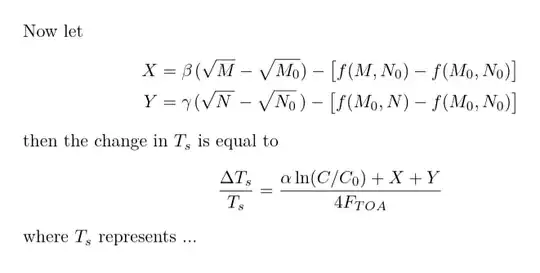
Where X and Y needs to be given better names depending on the contect. It looks like you are running some two dimensional iteration scheme, but without context it is hard to suggest better names.

^{While a minor detail look how nicely everything is aligned in the top two equations despite M and N having different widths..}

---

\documentclass[10pt,a4paper]{article}
\usepackage{mathtools}
\begin{document}
\noindent
Now let 
%
\bgroup
\newcommand{\NM}{\mathrlap{N}{\phantom{M}}}
\newcommand{\NMsqrt}{\mathrlap{\sqrt{N_0}}{\phantom{\sqrt{M_0}}}}
\begin{align}
    X &= \beta\mspace{2mu}(\sqrt{M} - \sqrt{M_0}) - \bigl[f(M, N_0) - f(M_0, N_0)\bigr]\
    Y &= \gamma\mspace{2mu}(\sqrt{\NM} - \NMsqrt) - \bigl[f(M_0, N) - f(M_0, N_0)\bigr]
\end{align}
\egroup
%
then the change in $T_s$ is equal to
%
\begin{equation}
\frac{\Delta T_s}{T_s}
  = \frac{\alpha \ln(C/C_0) + X + Y}{4F_{TOA}}
\end{equation}
%
where $T_s$ represents ...
\end{document}