This is not very difficult to draw in tikz. In my example I made a couple of functions (with math tikz library) that compute the coordinates of the intersection points of the tangent drawn from a x-axis given point to an ellipse (and a circle is an ellipse too). Then all I need is Thales' Intercept Theorem (and tikz calc library) and I get the following:
\documentclass[border=2mm]{standalone}
\usepackage {tikz}
\usetikzlibrary{calc}
\usetikzlibrary{math}
\tikzmath%
{%
function slope(\xp,\a,\k)
{% slope of the tangent form the point (xp,0) to the ellipse x^2/a^2+b^2/k^2a^2=1
return {\k\a/sqrt(\xp\xp-\a\a)};
};
function interx(\xp,\a,\k)
{% tangent point x (same tangent as above)
\mm = slope(\xp,\a,\k);
return {\mm\mm\xp/(\k\k+\mm\mm)};
};
function intery(\xp,\a,\k)
{% tangent point y (same tangent again)
return {slope(\xp,\a,\k)(\xp-interx(\xp,\a,\k))};
};
}
\begin{document}
\begin{tikzpicture}[line join=round]
% dimensions
\def\a {1} % cyan ellipse horizontal semi-axis
\def\k {2} % ratio between ellipses semi-axes, b/a
\def\xp{14} % point P, x coordinate (see below)
\def\re{0.75} % ratio between yellow an cyan ellipses
\def\yc{0.75} % ker circle center, y
\def\rc{0.5} % ker circle radius
\def\xc{4} % big circle center, x
% coordinates
\coordinate (P) at (\xp,0); % point P where the ellipses tangents meet
\coordinate (A0) at (0,0); % cyan ellipse, center
\coordinate (A1) at ({interx(\xp,\a,\k)},{ intery(\xp,\a,\k)}); % cyan ellipse, top tangent point
\coordinate (A2) at ({interx(\xp,\a,\k)},{-intery(\xp,\a,\k)}); % cyan ellipse, bottom tangent point
\coordinate (C0) at (0,-\yc); % ker circle center
\foreach\i in {0,1,2}
\coordinate (B\i) at ($(A\i)!1-\re!(P)$); % yellow ellipse points B0, B1, B2 (same as A0, A1, A2)
\coordinate (D0) at ($(B0)-(0,\yc)$); % 0
\coordinate (C1) at ({interx(\re\xp,\rc,1)},{ intery(\re\xp,\rc,1)-\yc}); % circle, top tangent point
\coordinate (C2) at ({interx(\re\xp,\rc,1)},{-intery(\re\xp,\rc,1)-\yc}); % circle, bottom tangent point
\coordinate (E0) at (\xc,0); % big circle center
% ellipses and circles
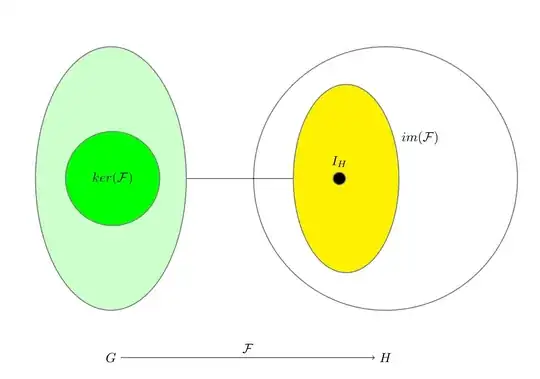
\draw[fill=cyan!40] (A0) ellipse (\a cm and \a\k cm) node (G) [yshift=-2cm,below] {$G$};
\draw[fill=yellow!40] (B0) ellipse (\re\a cm and \re\a\k cm) node [above] {$\mathrm{im},f$};
\draw[fill=green] (C0) circle (\rc) node {$\ker f$};
\draw (E0) circle (\k*\a) node (H) [yshift=-2cm,below] {$H$};
% lines
\draw (A1) -- (B1);
\draw (A2) -- (B2);
\draw (C1) -- (D0) -- (C2);
\draw[-latex] (G) -- (H) node [midway,below] {$f$};
\fill (D0) circle (1pt) node [above] {$0$};
\end{tikzpicture}
\end{document}



\draw (G.north) to (im.north);? – Torbjørn T. Jul 12 '21 at 16:31\draw (ker) +({atan(110pt/1.25cm)}: 1.25 ) -- (p); \draw (ker) +({-atan(110pt/1.25cm)}: 1.25 ) -- (p);– hpekristiansen Jul 12 '21 at 16:53ptandcm, unless there is some purpose. I would redo this figure intkz-euclide- I am almost sure that it can do tangents of ellipses. – hpekristiansen Jul 12 '21 at 16:56