How to make table size fit page?

Question

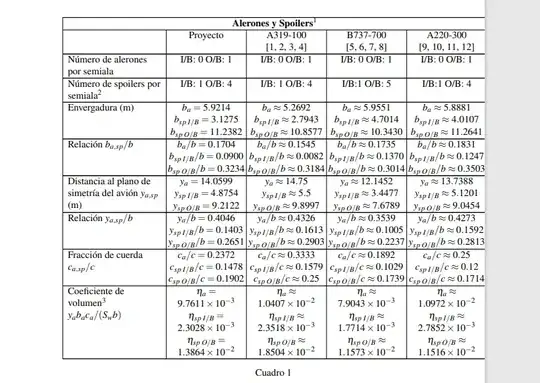
I have the following table, that compiles like this, not fitting on the page:

The code for it:

\begin{longtable}{ |L{4cm}|c|c|c|c| }
    \caption[Datos de los alerones y spoilers de aviones semejantes.]{\label{aler_spoil}}
    \endlastfoot
        \hline
        \multicolumn{5}{|c|}{\textbf{Alerones y Spoilers\footnote{Las definiciones son análogas a las dadas para dispositivos hipersustentadores.}}} \\
        \hline
        & Proyecto & \vtop{\hbox{\strut \makebox[2.5cm][c]{A319-100}\par }\hbox{\strut \makebox[2.5cm][c]{\cite{A319APM,JanesA319,A319TC,EurocontrolA319}}\par}} & \vtop{\hbox{\strut \makebox[2.5cm][c]{B737-700}\par }\hbox{\strut \makebox[2.5cm][c]{\cite{B737APM,JanesB737,B737TC,EurocontrolB737}}\par}} & \vtop{\hbox{\strut \makebox[2.5cm][c]{A220-300}\par }\hbox{\strut \makebox[2.5cm][c]{\cite{A220APM,JanesA220,A220TC,EurocontrolA220}}\par}} \\
        \hline
        Número de alerones por semiala & I/B: 0 O/B: 1 & I/B: 0 O/B: 1 & I/B: 0 O/B: 1 & I/B: 0 O/B: 1 \\
        \hline
        Número de spoilers por semiala\footnote{Al igual que con los slats, consideramos que los spoilers externos conforman un único dispositivo. De esta manera, empleamos los subíndices $sp\;I/B$ y $sp\;O/B$ para referirnos a los spoilers interno y externos, respectivamente.} & I/B: 1 O/B: 4 & I/B: 1 O/B: 4 & I/B:1 O/B: 5 & I/B:1 O/B: 4 \\
        \hline
        Envergadura (m) & \vtop{\hbox{\strut \makebox[3cm][c]{$b_a = 5.9214$}\par }\hbox{\strut \makebox[3cm][c]{$b_{sp\;I/B} = 3.1275$}\par}\hbox{\strut \makebox[3cm][c]{$b_{sp\;O/B} = 11.2382$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$b_a \approx 5.2692$}\par }\hbox{\strut \makebox[3cm][c]{$b_{sp\;I/B} \approx 2.7943$}\par}\hbox{\strut \makebox[3cm][c]{$b_{sp\;O/B} \approx 10.8577$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$b_a \approx 5.9551$}\par }\hbox{\strut \makebox[3cm][c]{$b_{sp\;I/B} \approx 4.7014$}\par}\hbox{\strut \makebox[3cm][c]{$b_{sp\;O/B} \approx 10.3430$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$b_a \approx 5.8881$}\par }\hbox{\strut \makebox[3cm][c]{$b_{sp\;I/B} \approx 4.0107$}\par}\hbox{\strut \makebox[3cm][c]{$b_{sp\;O/B} \approx 11.2641$}\par}} \\
        \hline
        Relación $b_{a,sp}/b$ & \vtop{\hbox{\strut \makebox[3cm][c]{$b_a/b = 0.1704$}\par }\hbox{\strut \makebox[3cm][c]{$b_{sp\;I/B}/b = 0.0900$}\par}\hbox{\strut \makebox[3cm][c]{$b_{sp\;O/B}/b = 0.3234$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$b_a/b \approx 0.1545$}\par }\hbox{\strut \makebox[3cm][c]{$b_{sp\;I/B}/b \approx 0.0082$}\par}\hbox{\strut \makebox[3cm][c]{$b_{sp\;O/B}/b \approx 0.3184$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$b_a/b \approx 0.1735$}\par }\hbox{\strut \makebox[3cm][c]{$b_{sp\;I/B}/b \approx 0.1370$}\par}\hbox{\strut \makebox[3cm][c]{$b_{sp\;O/B}/b \approx 0.3014$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$b_a/b \approx 0.1831$}\par }\hbox{\strut \makebox[3cm][c]{$b_{sp\;I/B}/b \approx 0.1247$}\par}\hbox{\strut \makebox[3cm][c]{$b_{sp\;O/B}/b \approx 0.3503$}\par}} \\
        \hline
        Distancia al plano de simetría del avión $y_{a,sp}$ (m) & \vtop{\hbox{\strut \makebox[3cm][c]{$y_a = 14.0599$}\par }\hbox{\strut \makebox[3cm][c]{$y_{sp\;I/B} = 4.8754$}\par}\hbox{\strut \makebox[3cm][c]{$y_{sp\;O/B} = 9.2122$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$y_a \approx 14.75$}\par }\hbox{\strut \makebox[3cm][c]{$y_{sp\;I/B} \approx 5.5$}\par}\hbox{\strut \makebox[3cm][c]{$y_{sp\;O/B} \approx 9.8997$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$y_a \approx 12.1452$}\par }\hbox{\strut \makebox[3cm][c]{$y_{sp\;I/B} \approx 3.4477$}\par}\hbox{\strut \makebox[3cm][c]{$y_{sp\;O/B} \approx 7.6789$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$y_a \approx 13.7388$}\par }\hbox{\strut \makebox[3cm][c]{$y_{sp\;I/B} \approx 5.1201$}\par}\hbox{\strut \makebox[3cm][c]{$y_{sp\;O/B} \approx 9.0454$}\par}} \\
        \hline
        Relación $y_{a,sp}/b$ & \vtop{\hbox{\strut \makebox[3cm][c]{$y_a/b = 0.4046$}\par }\hbox{\strut \makebox[3cm][c]{$y_{sp\;I/B}/b = 0.1403$}\par}\hbox{\strut \makebox[3cm][c]{$y_{sp\;O/B}/b = 0.2651$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$y_a/b \approx 0.4326$}\par }\hbox{\strut \makebox[3cm][c]{$y_{sp\;I/B}/b \approx 0.1613$}\par}\hbox{\strut \makebox[3cm][c]{$y_{sp\;O/B}/b \approx 0.2903$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$y_a/b \approx 0.3539$}\par }\hbox{\strut \makebox[3cm][c]{$y_{sp\;I/B}/b \approx 0.1005$}\par}\hbox{\strut \makebox[3cm][c]{$y_{sp\;O/B}/b \approx 0.2237$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$y_a/b \approx 0.4273$}\par }\hbox{\strut \makebox[3cm][c]{$y_{sp\;I/B}/b \approx 0.1592$}\par}\hbox{\strut \makebox[3cm][c]{$y_{sp\;O/B}/b \approx 0.2813$}\par}} \\
        \hline
        Fracción de cuerda $c_{a,sp}/c$ & \vtop{\hbox{\strut \makebox[3cm][c]{$c_a/c = 0.2372$}\par }\hbox{\strut \makebox[3cm][c]{$c_{sp\;I/B}/c = 0.1478$}\par}\hbox{\strut \makebox[3cm][c]{$c_{sp\;O/B}/c = 0.1902$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$c_a/c \approx 0.3333$}\par }\hbox{\strut \makebox[3cm][c]{$c_{sp\;I/B}/c \approx 0.1579$}\par}\hbox{\strut \makebox[3cm][c]{$c_{sp\;O/B}/c \approx 0.25$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$c_a/c \approx 0.1892$}\par }\hbox{\strut \makebox[3cm][c]{$c_{sp\;I/B}/c \approx 0.1029$}\par}\hbox{\strut \makebox[3cm][c]{$c_{sp\;O/B}/c \approx 0.1739$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$c_a/c \approx 0.25$}\par }\hbox{\strut \makebox[3cm][c]{$c_{sp\;I/B}/c \approx 0.12$}\par}\hbox{\strut \makebox[3cm][c]{$c_{sp\;O/B}/c \approx 0.1714$}\par}} \\
        \hline
        Coeficiente de volumen\footnote{Para calcular el coeficiente de volumen, hemos tomado $c_{a,sp}$ como la cuerda del elemento en el punto medio de su semienvergadura.} $y_ab_ac_a/(S_wb)$ & \vtop{\hbox{\strut \makebox[3cm][c]{$\eta_a =$}\par}\hbox{\strut \makebox[3cm][c]{$ \num{9.7611e-3}$}\par}\hbox{\strut \makebox[3cm][c]{$\eta_{sp\;I/B} =$}\par}\hbox{\strut \makebox[3cm][c]{$\num{2.3028e-3}$}\par}\hbox{\strut \makebox[3cm][c]{$\eta_{sp\;O/B} =$}\par}\hbox{\strut \makebox[3cm][c]{$\num{1.3864e-2}$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$\eta_a \approx$}\par}\hbox{\strut \makebox[3cm][c]{$ \num{1.0407e-2}$}\par}\hbox{\strut \makebox[3cm][c]{$\eta_{sp\;I/B} \approx$}\par}\hbox{\strut \makebox[3cm][c]{$\num{2.3518e-3}$}\par}\hbox{\strut \makebox[3cm][c]{$\eta_{sp\;O/B} \approx$}\par}\hbox{\strut \makebox[3cm][c]{$\num{1.8504e-2}$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$\eta_a \approx$}\par }\hbox{\strut \makebox[3cm][c]{$\num{7.9043e-3}$}\par}\hbox{\strut \makebox[3cm][c]{$\eta_{sp\;I/B} \approx$}\par}\hbox{\strut \makebox[3cm][c]{$\num{1.7714e-3}$}\par}\hbox{\strut \makebox[3cm][c]{$\eta_{sp\;O/B} \approx$}\par}\hbox{\strut \makebox[3cm][c]{$\num{1.1573e-2}$}\par}} & \vtop{\hbox{\strut \makebox[3cm][c]{$\eta_a \approx$}\par }\hbox{\strut \makebox[3cm][c]{$\num{1.0972e-2}$}\par}\hbox{\strut \makebox[3cm][c]{$\eta_{sp\;I/B} \approx$}\par}\hbox{\strut \makebox[3cm][c]{$\num{ 2.7852e-3}$}\par}\hbox{\strut \makebox[3cm][c]{$\eta_{sp\;O/B} \approx$}\par}\hbox{\strut \makebox[3cm][c]{$\num{1.1516e-2}$}\par}} \\
        \hline
\end{longtable}

What is an aesthetic solution to making this table fit within the margins?