How to draw this cube with holes?

Question

I am trying to draw this cube

I tried

\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\begin{document}
    \tdplotsetmaincoords{60}{120}
    \begin{tikzpicture}[tdplot_main_coords,declare function={a=3;
        }]
        \path 
        (a,-a,-a) coordinate (A)
        (a,a,-a) coordinate (B)
        (-a,a,-a) coordinate (C)
        (-a,-a,-a) coordinate (D)
        (a,-a,a) coordinate (E)
        (a,a,a) coordinate (F)
        (-a,a,a) coordinate (G)
        (-a,-a,a) coordinate (H)
        (0,0,0)  coordinate (O)
        ;
\draw (E) -- (A) -- (B) --(C) -- (G) -- (H) -- (E) (E) -- (F) -- (G) (B) -- (F);
%\path foreach \p/\g in {A/-90,B/90,C/0,D/0,E/0,F/0,G/0,H/0}{(\p)node{}+(\g:2.5mm) node{$\p$}}; 
\end{tikzpicture}
\end{document}

And got

How can I get cube with holes?

You could probably take some good advice in this question and its answer, especially the \mengersponge command you'll find there. — SebGlav, Sep 18 '21 at 09:02

Juan Castaño · Accepted Answer · 2021-09-18T20:33:11.360

With TikZ this is easy to draw using pics, styles and the 3d library:

\documentclass[tikz,border=2mm]{standalone}
\usetikzlibrary{3d}
\tikzset
{%
  front face/.style={fill=gray!20,canvas is xy plane at z=1},
  up    face/.style={fill=gray!50,canvas is xz plane at y=1},
  east  face/.style={fill=gray!80,canvas is yz plane at x=1},
  pics/square/.style={
    code={\draw[fill=white,even odd rule] (0,0) rectangle (3,3) (1,1) rectangle (2,2);}},
}
\begin{document}
\begin{tikzpicture}
\foreach\i in {0,1} \foreach\s in {front face, up face, east face}
  \draw[\s] (\i,1-\i) rectangle ++(1,1);
\foreach\i in {1,2} \foreach\s in {front face, up face, east face}
  \draw[\s] (\i,3-\i) rectangle ++(1,1);
\pic[canvas is xy plane at z=3] {square};
\pic[canvas is xz plane at y=3] {square};
\pic[canvas is yz plane at x=3] {square};
\end{tikzpicture}
\end{document}

Update: An animated version. I shifted all the points and changed the perspective, but the rest is the same:

\documentclass     {beamer}
\usepackage        {tikz}
\usetikzlibrary    {3d,perspective}
% beamer configuration
\setbeamertemplate {navigation symbols}{}
\tikzset
{%
      up face/.style={fill=gray!30,canvas is xy plane at z=-0.5},
  pics/square/.style={code={\draw[fill=white,even odd rule] (-1.5,-1.5) rectangle (1.5,1.5)
                                                            (-0.5,-0.5) rectangle (0.5,0.5);}},
}
\begin{document}
\begin{frame}
\foreach\i in{1,...,18}
{
  \only<\i>
  {
    \begin{figure}\centering
    \begin{tikzpicture}[line cap=round,line join=round,isometric view,rotate around z=5\i-45]
    \pgfmathsetmacro\lc{50+2\i} % left  color proportion
    \pgfmathsetmacro\rc{86-2*\i} % right color proportion
    \tikzset
    {
      left  face/.style={fill=gray!\lc,canvas is xz plane at y=0.5},
      right face/.style={fill=gray!\rc,canvas is yz plane at x=0.5},
    }
    \useasboundingbox (0,0) circle (3cm);
    \draw[thick,red] (0,0,-4) -- (0,0,-1.5);
    \foreach\i in {0,1} 
    {

      \draw[up    face] (0.5-\i,-0.5+\i) rectangle ++(1,1);
      \draw[left  face] (0.5-\i,-0.5-\i) rectangle ++(1,1);
      \draw[right face] (0.5-\i,-0.5-\i) rectangle ++(1,1);
    }
    \draw[thick,red] (0,0,-1.5) -- (0,0,-0.5);
    \foreach\i in {0,1} 
    {
      \draw[up    face] (-1.5+\i,-0.5-\i) rectangle ++(1,1);
      \draw[left  face] (-1.5+\i,-0.5+\i) rectangle ++(1,1);
      \draw[right face] (-1.5+\i,-0.5+\i) rectangle ++(1,1);
    }
    \draw[thick,red] (0,0,-0.5) -- (0,0,1.5);
    \pic[canvas is xy plane at z= 1.5] at (0,0) {square};
    \pic[canvas is xz plane at y=-1.5] at (0,0) {square};
    \pic[canvas is yz plane at x=-1.5] at (0,0) {square};
    \draw[thick,red] (0,0,1.5) -- (0,0,4);
    \end{tikzpicture}
    \end{figure}
  }
}
\end{frame}
\end{document}

A neat solution for sure! because all surfaces here are planes. Could you make the figure in different views? or better in animation? — Black Mild, Sep 18 '21 at 17:00
@BlackMild, not this way, that's for sure. But, I'll think about it. — Juan Castaño, Sep 18 '21 at 17:04
Very cool! So you defined isometric style of your own. Why did not you use [isometric view] or [3d view] , avaiable in Section 63.2 Setting the view of the current pgfmanual? — Black Mild, Sep 18 '21 at 18:13
@BlackMild, I'm used to draw with the axes in this way. The isometric view form perspective library changes the sign in x and y axes. It's true that it's all the same for this picture, but old habits... — Juan Castaño, Sep 18 '21 at 18:46

score 13 · Answer 2 · answered Sep 19 '21 at 21:48

With perspective projection and cosine lightening, in TikZ

\documentclass[border=9,tikz]{standalone}
\usepackage{tikz-3dplot}
\makeatletter
\def\camerax{0}\def\cameray{0}\def\cameraz{0}
\def\cameras{25}\def\camerad{50}
\let\oldpointxyz\pgfpointxyz
\def\perspectivepointxyz#1#2#3{
    \oldpointxyz{#1-\camerax}{#2-\cameray}{#3-\cameraz}%%% (x,y,z) is camera center
    \pgfmathsetmacro\depth{\rcarot\pgftemp@x+\rcbrot\pgftemp@y+\rccrot\pgftemp@z}
    \pgfmathsetlength\pgf@x{\pgf@x\cameras/(\camerad-\depth)}%%% camera scale and
    \pgfmathsetlength\pgf@y{\pgf@y\cameras/(\camerad-\depth)}%%% camera distance
}
\tikzset{
    at z/.code={
        \pgfmathsetmacro\innerprod{\rccrot100}\pgfkeysalso{fill=gray!\innerprod!light}
        \def\pgfpointxy##1##2{\perspectivepointxyz{##1}{##2}{#1}}
    },
    at y/.code={
        \pgfmathsetmacro\innerprod{\rcbrot100}\pgfkeysalso{fill=ycolor!\innerprod!light}
        \def\pgfpointxy##1##2{\perspectivepointxyz{##2}{#1}{##1}}
    },
    at x/.code={
        \pgfmathsetmacro\innerprod{\rcarot100}\pgfkeysalso{fill=xcolor!\innerprod!light}
        \def\pgfpointxy##1##2{\perspectivepointxyz{#1}{##1}{##2}}
    },
}
\def\face{\draw[fill=gray,even odd rule]}
\begin{document}
\foreach\leftcolor/\rightcolor in{cyan/magenta,magenta/yellow,yellow/cyan}{
    \colorlet{xcolor}{\leftcolor}
    \colorlet{ycolor}{\rightcolor}
    \def\Nframe{45}
    \foreach\frame in{1,...,\Nframe}{
        \tdplotsetmaincoords{48+30cos(360\frame/\Nframe)}{90+90*\frame/\Nframe}
        \tikz[tdplot_main_coords]{
            \draw[x=1cm,y=1cm]circle(9);
            \begin{scope}% inside and farther away from camera
                \colorlet{light}{black}
                \def\insidefarface{
                    (3,-9)--(-3,-9)--(-3,3)--(-9,3)--(-9,-3)--(3,-3)--(3,-9)
                }
                \face[at z=-3]\insidefarface;
                \face[at y=-3]\insidefarface;
                \face[at x=-3]\insidefarface;
                \face[at y=3]\insidefarface;
                \face[at x=3]\insidefarface;
            \end{scope}
            \begin{scope}% inside but closer to camera
                \colorlet{light}{black}
                \def\insidenearface{
                    (-3,9)--(3,9)--(3,-3)--(9,-3)--(9,3)--(-3,3)--(-3,9)
                }
                \face[at z=-3]\insidenearface;
                \face[at y=-3]\insidenearface;
                \face[at x=-3]\insidenearface;
                \face[at y=3]\insidenearface;
                \face[at x=3]\insidenearface;
            \end{scope}
            \begin{scope}% outside
                \colorlet{light}{gray}
                \def\outsideface{
                    (-9,-9)--(-9,9)--(9,9)--(9,-9)--(-9,-9)
                    (-3,-3)--(-3,3)--(3,3)--(3,-3)--(-3,-3)
                }
                \ifdim\rcbrot pt>\rcarot pt
                    \face[at x=9]\outsideface;
                    \face[at y=9]\outsideface;
                \else
                    \face[at y=9]\outsideface;
                    \face[at x=9]\outsideface;
                \fi
                \face[at z=9]\outsideface;
            \end{scope}
        }
    }
}
\end{document}

+1: Amazing job Symbol 1! – Dr. Manuel Kuehner Sep 19 '21 at 23:03 — Dr. Manuel Kuehner, Sep 19 '21 at 23:03

Black Mild · Answer 3 · 2021-09-19T04:01:18.040

New solution The extrude command from graph3 of Asymptote does the job well! (see my previous answer here): figure is composed by the inner surface and the outer surface.

I will make 3D animation later! But for now you can rotate the figure by hand (drag the left mouse): download this html file and open with some browser (Microsoft Edge, Google Chrome, etc). A taste of 3D!

Top-right view

Side view

Another view

The code:

// http://asymptote.ualberta.ca/
unitsize(1cm);
//import three;
import graph3;
currentprojection=orthographic((5,1.6,1.6),zoom=.85,center=true);
pen p=yellow;
// the inner surface
draw(extrude(plane(X,Y,X+Y)),p);
draw(extrude(plane(X,Y,X+Y+3Z),-Z),p);
draw(extrude(plane(Y,Z,Y+Z),X),p);
draw(extrude(plane(Y,Z,Y+Z+3X),-X),p);
draw(extrude(plane(Z,X,Z+X),Y),p);
draw(extrude(plane(Z,X,Z+X+3Y),-Y),p);
// the outer surface
draw(extrude(plane(3X,3Y,O),Z),p);
draw(extrude(plane(3X,3Y,3Z),-Z),p);
draw(extrude(plane(3Y,3Z,O),X),p);
draw(extrude(plane(3Y,3Z,3X),-X),p);
draw(extrude(plane(3Z,3X,O),Y),p);
draw(extrude(plane(3Z,3X,3Y),-Y),p);

Old solution I guess that you expect answers with other tools. Also @SebGlav cited a nice link. So here is my rough solution with Asymptote for comparison. My computer has weak graphic card, the display of color of the figure is a bit incorrect.

Some improvements on light are needed to make the figure more clearly. At least, the edges can be drawn. If anyone has suggestion of improvement with Asymptote, I am all ears.

// http://asymptote.ualberta.ca/
unitsize(1cm);
import three;
currentprojection=orthographic((1,.5,.4),zoom=.85,center=true);
pen p=white;
draw(xscale3(3)shift(0,1,1)unitcube,p);
draw(yscale3(3)shift(1,0,1)unitcube,p);
draw(zscale3(3)shift(1,1,0)unitcube,p);
draw(scale3(3)*unitcube,yellow+opacity(.5));

Update: for now you can rotate the figure by hand (drag the left mouse): download this html file https://www.dropbox.com/s/y05aa4g2nblnpa4/CubeWithHoles.html and open with some browser (Microsoft Edge, Google Chrome, etc). A taste of 3D! — Black Mild, Sep 19 '21 at 04:02

score 6 · Answer 4 · answered Sep 18 '21 at 15:31

Compile with Asymptote.

Note that the problem of opacity is still not implemented in Asymptote at present.

Compile at http://asymptote.ualberta.ca/

Specially, if you have a powerful computer, you will learn 3D Asymptote easily, otherwise you will get a common error in Asymptote is out of memory, :-). Sob!

// settings.render=10;
size(8cm);
import three;
currentprojection=orthographic((1,0.5,0.35));
currentlight=nolight;
// See three.asy
// Line 2012: restricted path3 unitsquare3=O--X--X+Y--Y--cycle;
path3 p1=unitsquare3;
path3 p2=shift(1/3*(X+Y))*scale3(1/3)*p1;
// transform3 t=scale(1.25,1,1);
surface s=surface(reverse(p1)^^p2,planar=true);
surface[] S={s,rotate(90,O,X)s,rotate(-90,O,Y)s
           ,shift(Z)s,rotate(90,X,X+Y)s,rotate(-90,Y,X+Y)s};
path3[] p3=p1^^p2;
path3[][] P={p3,rotate(90,O,X)p3,rotate(-90,O,Y)p3
           ,shift(Z)p3,rotate(90,X,X+Y)p3,rotate(-90,Y,X+Y)p3};
draw(S,white);
for (int i=0; i<P.length; ++i){ 
  draw(P[i][0],0.8bp+red);
  draw(P[i][1],0.8bp+blue);
}
surface s0=scale3(1/3)unitcube;
transform3[] T={identity4,shift(1/3X),shift(2/3X)
               ,shift(1/3Y),shift(2/3Y),shift(1/3X+2/3Y)
               ,shift(2/3X+1/3Y),shift(2/3(X+Y))};
for (transform3 i : T) draw(is0,white);
for (transform3 i : T) draw(shift(2/3Z)is0,white);
transform3 tt(real r)
{
  return rotate(r,1/2(X+Y),1/2(X+Y)+(0,0,1));
}
for (int i : new int[]{0,90,180,270})
{
  draw(tt(i)shift(1/3Z)*s0,white);
}
draw(shift(1/3(X+Y))scale(1/3,1/3,1)unitcube,invisible,0.8bp+blue);
draw(shift(1/3(Z+Y))scale(1,1/3,1/3)unitcube,invisible,0.8bp+blue);
draw(shift(1/3(X+Z))scale(1/3,1,1/3)*unitcube,invisible,0.8bp+blue);

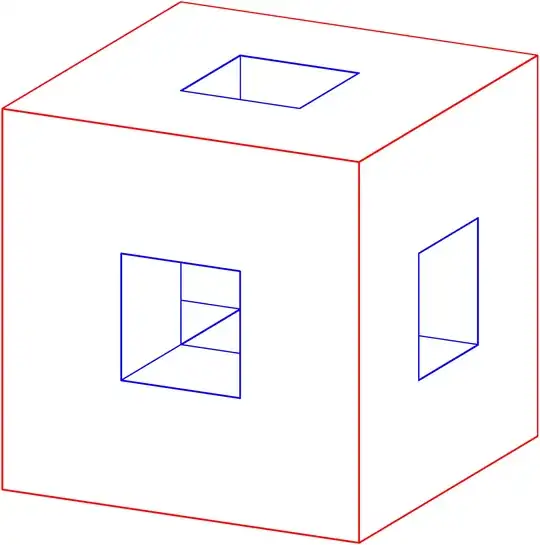
Animation:

import three;
import graph3;
currentprojection=orthographic((1,0.5,0.35));
currentlight=nolight;
size(8cm,0);
string[] files;
int numberofframes=72;
for (int i=0; i <= numberofframes; ++i)
{
files[i]="T"+(string) i;
picture pic;
// See three.asy
// Line 2012: restricted path3 unitsquare3=O--X--X+Y--Y--cycle;
path3 p1=unitsquare3;
path3 p2=shift(1/3(X+Y))scale3(1/3)*p1;
transform3 t=rotate(i*5,Z);
surface s=surface(reverse(p1)^^p2,planar=true);
surface[] S={s,rotate(90,O,X)s,rotate(-90,O,Y)s
           ,shift(Z)s,rotate(90,X,X+Y)s,rotate(-90,Y,X+Y)s};
path3[] p3=p1^^p2;
path3[][] P={p3,rotate(90,O,X)p3,rotate(-90,O,Y)p3
           ,shift(Z)p3,rotate(90,X,X+Y)p3,rotate(-90,Y,X+Y)p3};
draw(pic,tS,white);
for (int i=0; i<P.length; ++i){ 
  draw(pic,tP[i][0],0.8bp+red);
  draw(pic,t*P[i][1],0.8bp+blue);
}
surface s0=scale3(1/3)unitcube;
transform3[] T={identity4,shift(1/3X),shift(2/3X)
               ,shift(1/3Y),shift(2/3Y),shift(1/3X+2/3Y)
               ,shift(2/3X+1/3Y),shift(2/3(X+Y))};
for (transform3 i : T) draw(pic,tis0,white);
for (transform3 i : T) draw(pic,tshift(2/3Z)is0,white);
transform3 tt(real r)
{
  return rotate(r,1/2(X+Y),1/2(X+Y)+(0,0,1));
}
for (int i : new int[]{0,90,180,270})
{
  draw(pic,ttt(i)shift(1/3Z)s0,white);
}
draw(pic,tshift(1/3(X+Y))scale(1/3,1/3,1)unitcube,invisible,0.8bp+blue);
draw(pic,tshift(1/3(Z+Y))scale(1,1/3,1/3)unitcube,invisible,0.8bp+blue);
draw(pic,tshift(1/3(X+Z))scale(1/3,1,1/3)unitcube,invisible,0.8bp+blue);
xaxis3(pic,"$x$",-.5,2,Arrow3);
yaxis3(pic,"$y$",-2,2,Arrow3);
zaxis3(pic,"$z$",-.5,2,Arrow3);
add(pic);
shipout(files[i],bbox(invisible));
erase();
}

@BlackMild Thanks for your compliment! My code is still lengthy. — Nguyen Van Chi, Sep 18 '21 at 16:38

How to draw this cube with holes?

4 Answers4

Linked