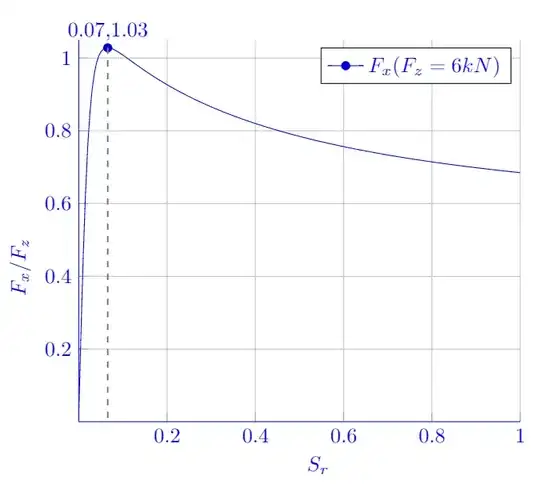
I would like to find the maximum of a curve and show the value as I have indicated in the picure below. I can't find any example in this forum that is applicable to my case.
\documentclass[border=5pt]{standalone}
\usepackage{tikz}
\usepackage{pgfplots}
\pgfplotsset{compat=newest}
\usepgfplotslibrary{units}
\begin{document}
\begin{tikzpicture}
\begin{axis}[change y base,
x unit= ,
% y SI prefix=kilo,
y unit= ,
xmin=0, xmax=1,
ymin=0, ymax=1.1,
% ytick={0,1000,...,6000},
xlabel=Degree,
ylabel=Force,
xlabel={$S_r$},
ylabel={$F_x/F_z$},
xlabel style={below right},
ylabel style={above left},
height=8cm,
width=9cm,
grid=minor,
samples=99,
trig format plots=rad
]
\newcommand\SV{80.1}
\newcommand\SH{0}
\newcommand\B{0.210}
\newcommand\C{1.67}
\newcommand\D{6090}
\newcommand\E{0.686}
\newcommand\Fz{6000}
\addplot[domain=0:1, blue, thick] {(\SV+\Dsin(\Catan(\B(1-\E)(x100+\SH)
+( atan(\B(x*100+\SH))
)
)
)
)/\Fz
};
\addlegendentry{$F_x(F_z=6kN)$}
\end{axis}
\end{tikzpicture}
\end{document}