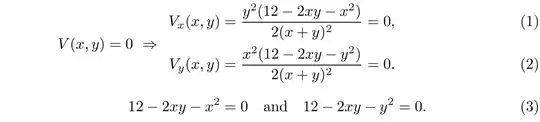2

I have the below code

\begin{gather} V(x,y) = 0 \Rightarrow \begin{aligned}
{V_x}(x,y) &= \frac{{{y^2}(12 - 2xy - {x^2})}}{{2{{(x + y)}^2}}} = 0,\\
{V_y}(x,y) &= \frac{{{x^2}(12 - 2xy - {y^2})}}{{2{{(x + y)}^2}}} = 0.
\end{aligned}\\
\Rightarrow 12-2xy-x^2 = 0\quad \text{and}\quad 12-2xy-y^2 = 0.
\end{gather}

How can I cross-reference the equation \frac{{{y^2}(12 - 2xy - {x^2})}}{{2{{(x + y)}^2}}} = 0?

Mico
  • 506,678
Dr. Kareem Elgindy
  • 93

2 Answers2

3

The following solution borrows heavily (steals??) from this answer of @egreg's to the question nested equations numbering.

enter image description here

\documentclass{article}
\usepackage{mathtools}
\begin{document}
\begin{align}
&\makebox[0pt][l]{\smash{\raisebox{-1\baselineskip}{%
  $\mathllap{V(x,y) = 0\ }\Rightarrow\quad$ }}}
   \hphantom{\Rightarrow\quad}
   V_x(x,y) = \frac{y^2(12 - 2xy - x^2)}{2(x + y)^2} = 0, \\
& \hphantom{\Rightarrow\quad}
  V_y(x,y) = \frac{x^2(12 - 2xy - y^2)}{2(x + y)^2} = 0.\\[2\jot]
&\Rightarrow 12-2xy-x^2 = 0 \quad \text{and}\quad 12-2xy-y^2 = 0.
\end{align}
\end{document}

Addendum: The OP has posted a follow-up request for a version of the three-equation group without a \Rightarrow at the start of the third line, and with the first = symbol in the third line aligned with the first = symbols in the two preceding lines. Here goes.

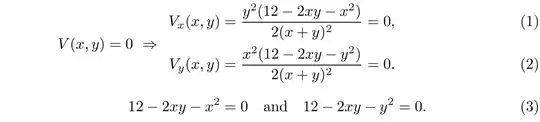
enter image description here

\documentclass{article}
\usepackage{mathtools,showframe}
\begin{document}
\begin{align}
\makebox[0pt][l]{\smash{\raisebox{-1\baselineskip}{%
    $\mathllap{V(x,y) = 0\ }\Rightarrow\quad$}}}
 \hphantom{\Rightarrow\quad}
   V_x(x,y) &= \frac{y^2(12 - 2xy - x^2)}{2(x + y)^2} = 0, \\
 \hphantom{\Rightarrow\quad}
  V_y(x,y) &= \frac{x^2(12 - 2xy - y^2)}{2(x + y)^2} = 0.\\[2\jot]
 12-2xy-x^2 &= 0 \quad \text{and}\quad 12-2xy-y^2 = 0.
\end{align}
\end{document}
Mico
  • 506,678
  • 1
    Wonderful solution. – Dr. Kareem Elgindy Nov 07 '21 at 17:10
  • @Dr.KareemElgindy - You're most welcome! If you believe that I've fully answered your question, I'd appreciate if you would "accept" my answer, by clicking on the green checkmark symbol. ;-) – Mico Nov 08 '21 at 07:57
  • 1
    Done bro. BTW, if I wanted to remove the right arrow from Eq. (3) and align the first equality of that line with the equality of V(x,y) in the above line, can you still do that while keeping everything else the same? – Dr. Kareem Elgindy Nov 08 '21 at 19:08
  • @Dr.KareemElgindy - Please see the addendum I just posted. – Mico Nov 08 '21 at 20:38
  • I highly appreciate your efforts @Mico. However, this is not exactly what I desired. I meant to align with V(x,y) not with V_x and V_y. – Dr. Kareem Elgindy Nov 09 '21 at 07:28
2

If I had to do this I'd probably use align and fudge the spacing...

enter image description here

\documentclass{article}

\usepackage{amsmath}


\begin{document}


gather
\begin{gather}
V(x,y) = 0 \Rightarrow \begin{aligned}
{V_x}(x,y) &= \frac{{{y^2}(12 - 2xy - {x^2})}}{{2{{(x + y)}^2}}} = 0,\
{V_y}(x,y) &= \frac{{{x^2}(12 - 2xy - {y^2})}}{{2{{(x + y)}^2}}} = 0.
\end{aligned}\
\Rightarrow 12-2xy-x^2 = 0\quad \text{and}\quad 12-2xy-y^2 = 0.
\end{gather}


align
\begin{align}
 &&{V_x}(x,y) &= \frac{{{y^2}(12 - 2xy - {x^2})}}{{2{{(x + y)}^2}}} = 0,\[-5pt]
V(x,y) = 0 \Rightarrow\notag\[-5pt]
&&{V_y}(x,y) &= \frac{{{x^2}(12 - 2xy - {y^2})}}{{2{{(x + y)}^2}}} = 0.\[5pt]
\Rightarrow&& 12-2xy-x^2 &= 0\quad \text{and}\quad 12-2xy-y^2 = 0.
\end{align}
\end{document}
David Carlisle
  • 757,742