I would like to encourage you to learn how to make use of LaTeX's approach -- its "way of thinking", if you prefer -- to separating content matters from formatting issues. While it involves a little bit more overhead at first, doing so immediately has huge payoffs in terms of getting access to all kinds of LaTeX packages that provide macros which perform all kinds of specific actions -- such as including the string label of an object that you wish to cross-reference. In other words, don't re-invent the wheel when a perfectly good one exists...
For instance, do learn how to use the machinery of the amsthm package to define and use theorem-like environments, including the "Definition" environment. If you do so, then creating a labeled cross-reference to a given definition is as trivially simple as replacing \ref{defn:eq_rel} with \cref{defn:eq_rel}, where \cref is a macro provided by the cleveref package.
By separating content matters from formatting issues, your code will quickly become more robust and more adaptable. For instance, if you decide that the definition of equivalence relations needs to be moved elsewhere in the document, not only will LaTeX automatically handle the change in the numbering of the definition, but any cross-references to that definition will also get adapted automatically.

\documentclass{report} % or some other suitable document class
\usepackage{enumitem} % more control over appearance of lists
\usepackage{amssymb} % for '\mathbb' macro
\usepackage{amsthm} % for '\newtheorem' macro
\usepackage[capitalize]{cleveref} % for '\cref' macro
\newtheorem{defn}{Definition}[section] % run this instruction *after* loading 'cleveref'.
\newcommand\boldemph[1]{\textup{\textbf{#1}}} % utility macro
\begin{document}
\setcounter{chapter}{2} % just for this example
\setcounter{section}{2}
\begin{defn} \label{defn:eq_rel} % use a descriptive label
Let $S$ be a set. A subset $R$ of $S \times S$ is called
an \boldemph{equivalence relation} on $S$ if
\begin{enumerate}[label=\upshape(\alph*)]
\item
for all $a \in S$, $(a,a) \in R$;
\item
for all $a,b \in S$, if $(a,b) \in R$, then $(b,a) \in R$;
\item
for all $a,b,c \in S$, if $(a,b) \in R$ and $(b,c) \in R$,
then $(a,c) \in R$.
\end{enumerate}
We will write $a \sim b$ to denote the fact that $(a,b) \in R$.
\end{defn}
\medskip\noindent
\dots
\bigskip
Let $x$, $x\in\mathbb{Z}$, such that $x\mid x^k$ and $x\mid x^j$.
Then $x\sim x$, and the equivalence relation is reflexive as
described by \cref{defn:eq_rel}.
\end{document}
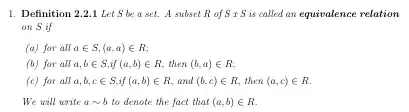
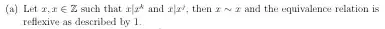


\ref{2.2.1}to magically become Definition 2.2.1. But then I don't understand why you're using\refin the first place. The point of\refis to allow Mico's answer to happen. If you're not doing that, then why bother, and not just type "as describe by Definition 2.2.1"? (Which would not let you learn from Mico, but you didn't know that you needed to learn that when you were using\ref.) – Teepeemm Nov 23 '21 at 19:16