Draw a line vertically above/below another through a given point

Question

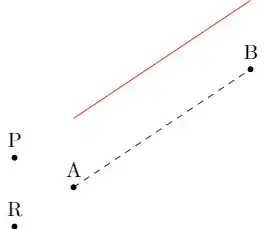
Given the points A, B and P below, I would like to draw a line parallel to AB and passes through P (or just points towards P if P is not between A and B on the x-axis as in this example). In other words, it is to shift AB up/down so that the shifted line is collinear with P.

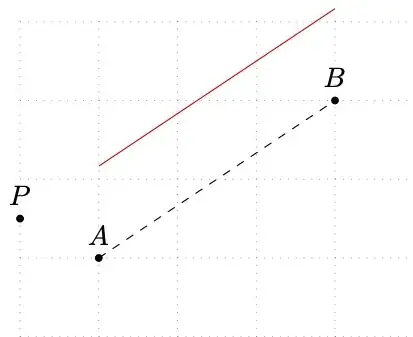
Desired output (the point R shown just for illustration):

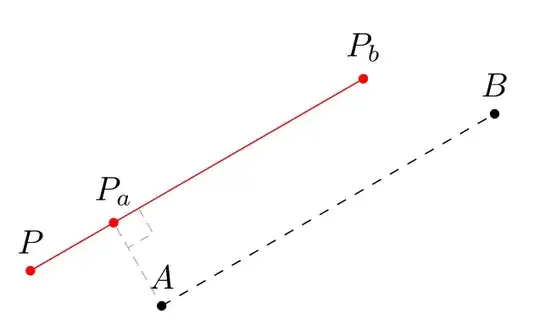
Below is what I currently have. In essence it is to project P vertically onto AB (call the projection R), then use tikz.calc to get the starting and ending points of the red line. I wonder if there is a simpler approach, where ideally I can do away with setting the dummy points Q and R? A similar problem is here but P has to be vertically above/below A or B in that question.

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}[dot/.style={circle,inner sep=1pt,fill,label={#1},name=#1}]
% define the points A, B, P
\draw[dashed] (0,0) node[dot=A]{}
    -- (3,2) node[dot=B]{}
    (-1,0.5) node[dot=P]{};

% find vertical projection of P on AB as R
\path (P) +(0,-0.1) coordinate(Q); %0.1 is an arbitary value
\node[dot=R] at (intersection of A--B and P--Q){}; %make R a coordinate in actual use

\draw[red] ($(A)+(P)-(R)$) -- ($(B)+(P)-(R)$);


\end{tikzpicture}
\end{document}

Answer 1

I think that you already gave the simplest and direct way. I just clean the code.

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}[dot/.style={circle,inner sep=1pt,fill=#1}]
\path
(0,0)     coordinate (A) node[dot]{} node[below]{$A$}
(3,2)     coordinate (B) node[dot]{} node[right]{$B$}
(-1,.5,0) coordinate (P) node[dot]{} node[above]{$P$}
+(90:1) coordinate (Pt)
(intersection of A--B and P--Pt) coordinate (R)
($(P)+(A)-(R)$) coordinate (Pa) node[dot=magenta]{} node[above left]{$P_a$}
($(P)+(B)-(R)$) coordinate (Pb) node[dot=magenta]{} node[above]{$P_b$}
;
\draw (A)--(B);
\draw[magenta] (Pa)--(Pb);
\end{tikzpicture}
\end{document}

Answer 2

By using polar coordinates the program becomes simple and short:

\documentclass[margin=3mm]{standalone}
\usepackage{tikz}
\usetikzlibrary{angles, % for show angle
                calc}
\begin{document}
    \begin{tikzpicture}[
dot/.style = {circle,inner sep=1pt,fill,label={[text=black]#1}, node contents={}}
                        ]
\draw[red] (0,0) node[dot=$P$] -- ++ (30:1) node (Pa) [dot=$P_a$] -- ++ (30:3) node (Pb) [dot=$P_b$];
\draw[dashed]   ($(Pa)!1cm!270:(Pb)$)       node (A)  [dot=$A$]   -- ++ (30:4) node[dot=$B$];
% for showing projection A on P -- Pb
\path[draw=gray, densely dashed, very thin] (Pa) -- (A) 
    pic [draw, angle radius=3mm] {right angle = Pb--Pa--A};
\end{tikzpicture}
\end{document}

Answer 3

This kind of problem is expected with tkz-euclide. There are several ways to get the result.

\documentclass{standalone}
\usepackage{tkz-euclide}
\begin{document}
\begin{tikzpicture} 
  \tkzDefPoints{0/0/A,5/2/B,-1/2/P}
  \tkzDefPointWith[colinear=at P,K=0.25](A,B) \tkzGetPoint{R}
  \tkzDefPointWith[colinear=at R](A,B) \tkzGetPoint{S}
  \tkzDrawPoints(A,B,P,R,S)
  \tkzDrawSegment(A,B)
  \tkzDrawLine[red,add=.1 and .1](R,S)
  \tkzLabelPoints(A,B,P,R,S)
\end{tikzpicture}
\end{document}

Answer 4

The idea is similar to yours with Asymptote.

size(200);
pair A=(0,0),B=(3,2);
pair P=(-1,0.5);
pair R=extension(A,B,P,P+(0,1));
draw(A--B,dashed);
draw(shift(P-R)*(A--B),red);
dot("$P$",P,N);
dot("$A$",A,N);
dot("$B$",B,N);
dot("$R$",R,N);

Output is like your second picture.

Answer 5

Using the tzplot package:

\documentclass[tikz]{standalone}
\usepackage{tzplot}
\begin{document}
\begin{tikzpicture}
\tzhelplines(-1,-1)(4,3)
\tzcoors*(0,0)(A){$A$}(3,2)(B){$B$}(-1,0.5)(P){$P$};
\tzlinedashed(B)
% get a slope and draw a line passing through (P)
\tzpointangle(A)(B){\myAng}
\tzLFnred{tan(\myAng)}[0:3]
\end{tikzpicture}
\end{document}