2

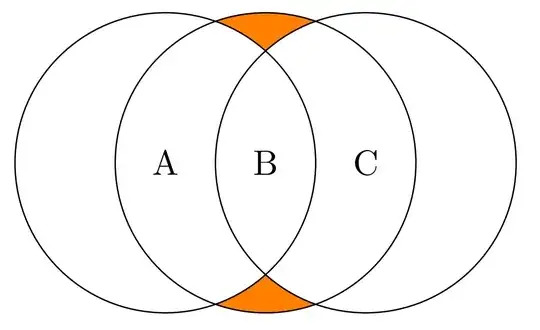
The code below does a good job of plotting $B / (A \cup C)$ provided $A \cap C = \emptyset$ but fails when $A$ and $C$ overlap.

How can I fix the lower panel so that only the part of $B$ that is outside $A$ and $C$ gets filled? If needed, it can be different from the solution for the top row, but one solution for both situations would be ideal.

I had recently asked a similar question where an answer showed how to make the top panel without filling in circles A and C in white, and am hoping it is possible to do the same for this new scenario.

\documentclass[tikz,border=1mm]{standalone}
\usetikzlibrary{math}

\begin{document}


\newcommand{\drawrow}[5]
           {
             \tikzmath{\xo=#1; \y=#2; \r=#3; \d=#4; \n=#5;};
             \foreach \x in {1,...,\n}{
               \draw ({\xo + (\x - 1) * \d}, \y) circle (\r) {};
             }
           }


\begin{tikzpicture}
  \tikzmath{\r = 1; \d = 1.2; \x = -\d; \y=0;}
  \def\A{({\x},\y) circle(\r)};
  \def\B{({\x+\d},{\y}) circle(\r)};
  \def\C{({\x+2\d},{\y}) circle(\r)};
  \begin{scope}
    \clip \B;
    \fill[lightgray, even odd rule] \B \A \C;
  \end{scope}
  \drawrow{\x}{\y}{\r}{\d}{3}
  \node at ({\x}, \y) {A};
  \node at ({\x+\d}, \y) {B};
  \node at ({\x+2\d}, \y) {C};


\tikzmath{\r = 1; \d = 0.8; \x = -\d; \y=-2.5;} %%%% <---- NOTE CHANGE IN \d 
  \def\A{({\x},\y) circle(\r)};
  \def\B{({\x+\d},{\y}) circle(\r)};
  \def\C{({\x+2\d},{\y}) circle(\r)};
  \begin{scope}
    \clip \B;
    \fill[lightgray, even odd rule] \B \A \C;
  \end{scope}
  \drawrow{\x}{\y}{\r}{\d}{3}
  \node at ({\x}, \y) {A};
  \node at ({\x+\d}, \y) {B};
  \node at ({\x+2\d}, \y) {C};


\end{tikzpicture}
\end{document}

enter image description here

ramzeek
  • 197
  • 6

2 Answers2

3

Using the reverse clip technique from How can I invert a 'clip' selection within TikZ? then this is quite easy. We reverse clip against the A and C paths, and clip against the B one.

It doesn't play well with the standalone class (due to using the current page node which doesn't seem to be defined properly - but I'm guessing that the actual document isn't a standalone one, if it is then there are ways around this) but with article then it is fine.

Couple of other minor things:

  1. There were a few stray ; in your code. Only path commands need to end with ;, other thing (such as \tikzmath) don't.
  2. The proper syntax for circles is circle[radius=..], you're using an old syntax which is deprecated.
  3. Rather than storing the whole paths in \A, \B, \C then I went for defining coordinates. With the labels, then it felt like the coordinates were more often re-used than the whole paths.
\documentclass{article}
%\url{https://tex.stackexchange.com/q/642950/86}
\usepackage{tikz}
\usetikzlibrary{math}

% reverse clip from https://tex.stackexchange.com/q/12010/86
\tikzset{
  reverse clip/.style={
    overlay,
    clip even odd rule,
    insert path={(current page.north east) --
      (current page.south east) --
      (current page.south west) --
      (current page.north west) --
      (current page.north east)}
  },
  clip even odd rule/.code={%
    \pgfseteorule
  },
}


\newcommand{\drawrow}[5]
{
  \tikzmath{\xo=#1; \y=#2; \r=#3; \d=#4; \n=#5;}
  \foreach \x in {1,...,\n}{
    % New syntax is circle[radius=...]
    % and the {} is unnecessary
    \draw ({\xo + (\x - 1) * \d}, \y) circle[radius=\r];
  }
}


\begin{document}


\begin{tikzpicture}[remember picture]
\tikzmath{\r = 1; \d = 1.2; \x = -\d; \y=0;}


\coordinate (A) at (\x,\y);
\coordinate (B) at (\x+\d,\y);
\coordinate (C) at (\x+2*\d,\y);


\begin{scope}
\clip[reverse clip] (A) circle[radius=\r];
\clip[reverse clip] (C) circle[radius=\r];
\clip (B) circle[radius=\r];
\fill[lightgray]
(B) circle[radius=\r]
(A) circle[radius=\r]
(C) circle[radius=\r];
\end{scope}
\drawrow{\x}{\y}{\r}{\d}{3}
\foreach \lbl in {A,B,C}
  {
    \node at (\lbl) {(\lbl)};
  }


\tikzmath{\r = 1; \d = 0.8; \x = -\d; \y=-2.5;} %%%% <---- NOTE CHANGE IN \d


\coordinate (A) at (\x,\y);
\coordinate (B) at (\x+\d,\y);
\coordinate (C) at (\x+2*\d,\y);


\begin{scope}
\clip[reverse clip] (A) circle[radius=\r];
\clip[reverse clip] (C) circle[radius=\r];
\clip (B) circle[radius=\r];
\fill[lightgray]
(B) circle[radius=\r]
(A) circle[radius=\r]
(C) circle[radius=\r];
\end{scope}
\drawrow{\x}{\y}{\r}{\d}{3}
\foreach \lbl in {A,B,C}
{
  \node at (\lbl) {(\lbl)};
}


\end{tikzpicture}
\end{document}

Reverse clipping with venn diagrams

Andrew Stacey
  • 153,724
  • 43
  • 389
  • 751
  • It can optionally be shortened to (current page.north east) rectangle (current page.south west) – hpekristiansen May 04 '22 at 21:15
  • +1 I have no problem using your code with standalone class. Defining a reverse clip/.style can indeed be powerfull, but for single use, I personally find it simpler to use a rectangle(or any other path) that incompases the wished clip. -that way there is also no need for current page. and there is no need for remember picture – hpekristiansen May 04 '22 at 21:18
  • 1
    @hpekristiansen The original goal was something that would work without needing to think about exactly how big to make the path (Jake's original version had a rectangle 1m by 1m) so while other options are possible, this is guaranteed to always work. If a containing rectangle is known then of course that can be used. I had issues with standalone when constructing this solution, but maybe it was something else that caused the problem - sometimes one doesn't test every possibility! – Andrew Stacey May 04 '22 at 22:25
  • Thank you @AndrewStacey, this approach is interesting and I would never have found the link you shared. I am finding that when I copy and paste your code, though, I get the opposite part being kept. That is, the part in the middle with the B label rather than the top and bottom of the circle. Also the first example only has the top right quadrant of the original area filled. Any thoughts why that is? – ramzeek May 05 '22 at 04:07
  • To add to my follow-up in the comment above, using overlay seems to correct the issue but it messes up the formatting of my document. – ramzeek May 05 '22 at 04:49
  • @ramzeek try using a "large" rectangle rather than the current page node, or use overlay just on the problematic paths. It may be related to the issues I was seeing with standalone in that the current page node isn't being properly defined. (Also, it does take at least two compilations to settle down so it's always worth compiling one time more after everything is put in place in the document) – Andrew Stacey May 05 '22 at 05:49
  • Thanks @AndrewStacey for following up. In the end, my depth of understanding of tikz just wasn't enough to figure out how to adjust your example. Still gave it a +1 though. – ramzeek May 08 '22 at 22:22
2

Things get a bit more complex here. I use calc and intersections library to do that.

complex circles intersections

\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{intersections,calc}

\begin{document}

    \begin{tikzpicture}
        \newcommand{\R}{15mm}
        \newcommand{\A}{(0,0) circle (\R)}
        \newcommand{\B}{(1,0) circle (\R)}
        \newcommand{\C}{(2,0) circle (\R)}


    \path[name path=A] \A;
    \path[name path=C] \C;
    \path [name intersections={of=A and C}];

    \begin{scope}
        \clip \B;
        \clip ($(intersection-1)+(-1,0)$) rectangle ++(2,1);
        \fill[orange, even odd rule] \A \B \C;
    \end{scope}

    \begin{scope}
        \clip \B;
        \clip ($(intersection-2)+(-1,0)$) rectangle ++(2,-1);
        \fill[orange, even odd rule] \A \B \C;
    \end{scope}

    \draw \A node {A} \B node {B} \C node {C};
\end{tikzpicture}



\end{document}
SebGlav
  • 19,186
  • 1
    I needed to modify slightly to work with \r and \d like in my example (as I need it in a function that is used multiple times) but once I figured that out, it worked like a charm. Thanks. (The change was basically along the lines of \clip ($(intersection-1)+(-\r,0)$) rectangle ++({2*\r},{\r})). – ramzeek May 08 '22 at 22:20