How to draw a path alternating in background and foreground?

Question

I would like to draw a spring which "wraps" arround a bar, meaning every alternating line should be drawn on the background. Is is possible to define a tikzstyle for this?

\documentclass[tikz, border=3mm]{standalone}
\usetikzlibrary{decorations.pathmorphing}
\usepackage{kinematikz}
\tikzset{
    spring/.style = {
        thick,decorate,green!40!black,decoration={zigzag,amplitude=13,segment length=12}
    },
}
\begin{document}
\begin{tikzpicture}
    \coordinate (P1) at (0,0);
    \coordinate (P2) at (5,0);
    \pic (bar) at (P1) {link bar generic=P2/0};
    \draw[spring] (P1) -- (P2);
\end{tikzpicture}
\end{document}

The kinematikz package is just for the bar pic.

I don't think you can expect this to be done automatically. You may need to draw a bit more manually than with a decoration. Maybe a foreach loop and some computations. — SebGlav, May 24 '22 at 11:52
See also: https://tex.stackexchange.com/questions/32297/modify-tikz-coil-decoration — hpekristiansen, May 24 '22 at 12:23

Tom · Accepted Answer · 2022-05-25T06:15:36.083

2

This might not be an elegant way. But seems worked. You could declare two decoration: one for right slanted spring , one for left slanted spring. Then put one before the bar, the other one after the bar (right slanted spring on the foreground could be better).

\documentclass[tikz, border=3mm]{standalone}
\usetikzlibrary{decorations.pathmorphing}
\usepackage{kinematikz}
\pgfdeclaredecoration{lspr}{initial}
{
\state{initial}[width=12.5pt]
{
\pgfpathmoveto{\pgfpoint{4pt}{12pt}}
\pgfpathlineto{\pgfpoint{8.5pt}{-12pt}}
}
\state{final}
{
\pgfpathmoveto{\pgfpointdecoratedpathlast}
}
}
\pgfdeclaredecoration{rspr}{initial}
{
\state{initial}[width=12.5pt]
{
\pgfpathlineto{\pgfpoint{4pt}{12pt}}
\pgfpathmoveto{\pgfpoint{8.5pt}{-12pt}}
\pgfpathlineto{\pgfpoint{12.5pt}{0pt}}
}
\state{final}
{
\pgfpathlineto{\pgfpointdecoratedpathlast}
}
}
\tikzset{
    rspring/.style = {
        thick,decorate,green!40!black,decoration={rspr, pre length=0.3cm}
    },
    lspring/.style = {
        thick,decorate,green!40!black,decoration={lspr, pre length=0.3cm}
    },
}
\begin{document}
\begin{tikzpicture}
    \coordinate (P1) at (0,0);
    \coordinate (P2) at (5,0);
    \draw[lspring] (P1) -- (P2);
    \pic (bar) at (P1) {link bar generic=P2/0};
    \draw[rspring] (P1) -- (P2);
\end{tikzpicture}
\end{document}

edited May 25 '22 at 06:15

answered May 24 '22 at 09:35

Tom

7,318
4
21

This works great! I would like to make these decorations accept optional values like amplitude or segment length. Can you tell where I can find information for that? – marv May 25 '22 at 05:18
@marv Not quite sure about that. You could took a look the pgf manual "https://ctan.mirror.globo.tech/graphics/pgf/base/doc/pgfmanual.pdf" page. 638 and 1108. Or the link in hpekristiansen's comment. – Tom May 25 '22 at 05:37
Thanks, the comment link is quite usefull. One more question? Why did you add 0.5pt to all the lengths? – marv May 25 '22 at 05:40
@marv Those just through trial and error to make each segments looks in a good ratios. You can edit them to make the results as you wanted. But at least keep them same for both left and right slanted spring. – Tom May 25 '22 at 05:45
With the references you provided it was very easy to parameterize the defintions of the decorations. I have posted the result as a separate answer. Thanks again for the help! – marv May 25 '22 at 06:10
@marv That's nice. I think put some 'pre length=' options will make it looks even better. see my new edits in the answer. – Tom May 25 '22 at 06:16
Great! The only thing I can still think of would be a method which automatically slightly adjusts the segment length such that the post length matches the desired pre length. But it is not that hard to it manually,... – marv May 25 '22 at 06:21

score 2 · Answer 2 · answered May 25 '22 at 06:05

Just an addition to @Tom's very nice answer. With these definitions, it is possible to parameterize the decorations using amplitude and segmengt length. Their result is stored in the TeX-dimensions \pgfdecorationsegmentamplitude and \pgfdecorationsegmentlength respectively. I also added an argument to the style defintions, which makes it possible to locally overwrite the default values.

\documentclass[tikz, border=3mm]{standalone}
\usetikzlibrary{decorations.pathmorphing}
\usepackage{kinematikz}
\pgfdeclaredecoration{lspr}{initial}
{
    \state{initial}[width=\pgfdecorationsegmentlength]
    {
        \pgfpathmoveto{\pgfpoint{\pgfdecorationsegmentlength/3}{\pgfdecorationsegmentamplitude}}
        \pgfpathlineto{\pgfpoint{\pgfdecorationsegmentlength/3*2}{-\pgfdecorationsegmentamplitude}}
    }
    \state{final}
    {
        \pgfpathmoveto{\pgfpointdecoratedpathlast}
    }
}
\pgfdeclaredecoration{rspr}{initial}
{
    \state{initial}[width=\pgfdecorationsegmentlength]
    {
        \pgfpathlineto{\pgfpoint{\pgfdecorationsegmentlength/3}{\pgfdecorationsegmentamplitude}}
        \pgfpathmoveto{\pgfpoint{\pgfdecorationsegmentlength/3*2}{-\pgfdecorationsegmentamplitude}}
        \pgfpathlineto{\pgfpoint{\pgfdecorationsegmentlength}{0pt}}
    }
    \state{final}
    {
        \pgfpathlineto{\pgfpointdecoratedpathlast}
    }
}
\tikzset{
    rspring/.style = {
        thick,decorate,green!40!black,decoration={rspr, amplitude=12pt, segment length=12pt, #1}
    },
    lspring/.style = {
        thick,decorate,green!40!black,decoration={lspr, amplitude=12pt, segment length=12pt, #1}
    },
}
\begin{document}
\begin{tikzpicture}
    \coordinate (P1) at (0,0);
    \coordinate (P2) at (5,0);
    \draw[lspring] (P1) -- (P2);
    \pic (bar) at (P1) {link bar generic=P2/0};
    \draw[rspring] (P1) -- (P2);
\begin{scope}[yshift=-1.2cm]
    \coordinate (P3) at (0,0);
    \coordinate (P4) at (5,0);
    \draw[lspring={amplitude=14pt, segment length=17pt}] (P3) -- (P4);
    \pic (bar) at (P3) {link bar generic=P4/0};
    \draw[rspring={amplitude=14pt, segment length=17pt}] (P3) -- (P4);
\end{scope}

\end{tikzpicture}
\end{document}

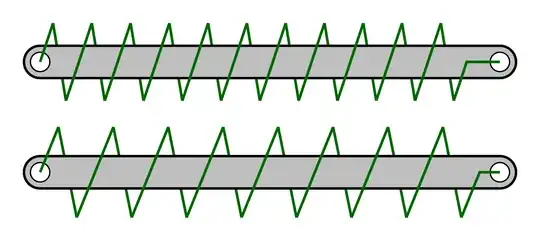
I am once again amazed how easy and flexible TikZ/PGF is!

How to draw a path alternating in background and foreground?

2 Answers2