0

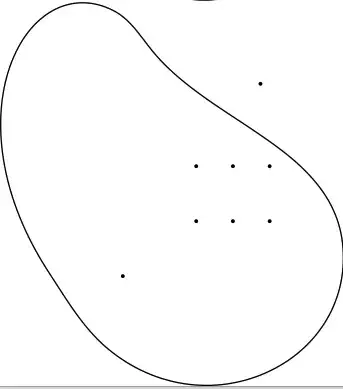
I am trying to adapt this metapost patatoid generator to fit a list of pairs given to a macro. To that purpose I loop through the list of pairs and determine the greatest x and y distances between all points with their coordinates. Then, I the the patatoid generator with the given width and height and shift it at the lowest coordinates to fit (almost) them all.

def drawlistofpoints(suffix p) =
  numeric i ; i := 0 ;
  forever:
    if known p[i]:
      drawdot p[i] withpen pencircle scaled 3pt ;
      i := i+1 ;
    fi ;
    exitif unknown p[i] ;
  endfor ;
enddef ;

vardef patatoid(expr w,h,x,y) =
  hide(
    numeric i,maxi,maxd ; i:=0; maxd := 0 ;
    numeric dist[] ;
    pair tmpp[] ;
    path sq, p ;
    sq := unitsquare xyscaled (w,h) shifted (x, y) ;
    for i = 0 upto 3:
        tmpp[i] := point (i + uniformdeviate(1)) of sq ;
    endfor ;
    tmpp[4] := tmpp[0] ;
    for i= 0 upto 3 :
        dist[i] := abs(tmpp[i+1] - tmpp[i]) ;
        if (dist[i] > maxd) :
            maxd := dist[i] ;
            maxi := i ;
        fi ;
    endfor ;
    p := for i = 0 upto maxi : tmpp[i] .. endfor (uniformdeviate(1))[tmpp[maxi],tmpp[maxi+1]] for i = maxi + 1 upto 3: .. tmpp[i] endfor .. cycle ;
  )
  p
enddef ;


def drawset(suffix p)=
  numeric i,w,h,lx,hx,ly,hy; i:=0; w:=0; h:=0; lx:=0; hx:=0; ly:=0; hy:=0;
  numeric offset ; offset = 2cm ;
  forever:
    if known p[i]: % this is a naive approach
      if (xpart p[i]) < lx: lx := (xpart p[i]); fi
      if (xpart p[i]) > hx: hx := (xpart p[i]); fi
      if (ypart p[i]) < ly: ly := (ypart p[i]); fi
      if (ypart p[i]) > hy: hy := (ypart p[i]); fi
      i:=i+1;
    fi
    exitif unknown p[i];
  endfor ;
  hx := hx+offset ; lx := lx-offset ; hy := hy+offset ; ly := ly-offset ;
  w := abs(hx - lx) ; h := abs(hy - ly) ;


draw patatoid(w,h,lx,ly) withpen pencircle scaled 1pt ;
  drawlistofpoints(p) ;
enddef ;

However, if a point have "unusual" coordinates and is not packed with the others it will finish outside of the patatoid:

\startTEXpage
  \startMPcode
    pair a,b,c,d,e,f, g,h;
    a := (0.5cm,0.75cm) ; b := (1.5cm,0.75cm) ; c := (2.5cm,0.75cm) ;
    d := (0.5cm,2.25cm) ; e := (1.5cm,2.25cm) ; f := (2.5cm,2.25cm) ;
    g := (2.25cm,4.5cm) ; h := (-1.5cm,-0.75cm) ;

pair points[];
points[0] := a ;
points[1] := b ;
points[2] := c ;
points[3] := d ;
points[4] := e ;
points[5] := f ;
points[6] := g ;
points[7] := h ;

drawset(points) ;



\stopMPcode
\stopTEXpage

How can I make sure to fit them all?

enter image description here enter image description here

  • Well, the patatoid is clearly not covering the rectangle that it is defined from, so you will have to give up something. Perhaps you start from the wrong end. – mickep Jun 02 '22 at 15:26
  • Can you please elaborate on "Perhaps you start from the wrong end."? –  Jun 02 '22 at 15:45
  • If you want to construct a curve that includes points in a certain rectangle, then it looks wrong to use a curve that by its definition do not cover the rectangle. So, what are you trying to do (on a higher level, perhaps)? – mickep Jun 02 '22 at 16:44
  • Imagine a blackboard where you want to draw, maybe a bijective map, and where you have a bunch of elements (represented by points (or pairs here)) of two sets A and B. The first step (way before drawing the map arrows) is to "circle" those elements to know which ones are elements of the A set and which other ones are elements of the B set. What I want here is to fake that patatoid shape we could create by hand on the blackboard. –  Jun 02 '22 at 16:59
  • Well, you could start with the patatoid, and then randomly generate points and test if they are inside. Loop until you have as many points as you wish. But not sure that would give you what you want. – mickep Jun 02 '22 at 17:36

1 Answers1

0

Here is a different implementation.

enter image description here

This is wrapped up in luamplib, so compile with lualatex, or adapt it to work with your Context environment.

\documentclass[border=5mm]{standalone}
\usepackage{luamplib}
\begin{document} 
\begin{mplibcode}
beginfig(1);

pair p[];
for i=1 upto 10:
    p[i] = 21(normaldeviate, normaldeviate);
endfor

picture dots; dots = image(
numeric i; i = 0;
forever:
    exitif not known p[incr i];
    draw p[i] withpen pencircle scaled 3;
endfor);

pair o; o = center dots;
path spud;
spud = for i=1/4 step 1/2 until 4:
   (5/4 + uniformdeviate 1/2)[o, point i of bbox dots] ..
endfor cycle;

fill spud withcolor 1/256(239, 234, 181);
draw spud;
draw dots;




endfig;
\end{mplibcode}
\end{document}

Notes

My approach here is

  • capture 10 dots in random places as p1, p2, p3 etc

  • save a drawing of all the dots as a <picture> variable

  • then step round the bounding box of the picture using the mediation syntax to find a point a random distance beyond the bbox. The expression (5/4 + uniformdeviate 1/2) yields a random number between 1.25 and 1.75, and since o is defined as the center of all the dots, 1.5[o, point i of bbox dots] yields a point that must be beyond the bbox.

  • and the clever bit is starting at point 1/4 and stepping 1/2 each time, so that we avoid the corners; this makes the random shape more potato-like.

  • I found the potato color 1/256(239, 234, 181) from searching the web.

A couple of other points of syntax:

  • If i is numeric, then incr i will increment it in place. There is also decr i which does the opposite. The implementation in plain.mp is very clever:

      % special operators
  vardef incr suffix $ = $:=$+1; $ enddef;
  vardef decr suffix $ = $:=$-1; $ enddef;

  • In Metapost (unlike in Metafont) drawdot <pair> is exactly equivalent to draw <pair>.

Some more detail

What's going on in these lines?

path spud;
spud = for i=1/4 step 1/2 until 4:
  (5/4 + uniformdeviate 1/2)[o, point i of bbox dots] ..
endfor cycle;

This loop is generating the outline path for the potato shape. (The word "spud" is British slang for a potato.) This is an in-line loop; Metapost expands the loop as part of making the definition, so it expands into:

spud = (1.25 + uniformdeviate 0.5)[o, point 0.25 of bbox dots] ..
       (1.25 + uniformdeviate 0.5)[o, point 0.75 of bbox dots] ..
       (1.25 + uniformdeviate 0.5)[o, point 1.25 of bbox dots] ..
       (1.25 + uniformdeviate 0.5)[o, point 1.75 of bbox dots] ..
       (1.25 + uniformdeviate 0.5)[o, point 2.25 of bbox dots] ..
       (1.25 + uniformdeviate 0.5)[o, point 2.75 of bbox dots] ..
       (1.25 + uniformdeviate 0.5)[o, point 3.25 of bbox dots] ..
       (1.25 + uniformdeviate 0.5)[o, point 3.75 of bbox dots] .. cycle;

which expands into something like this (although obviously, the uniformdeviate calls will be different each time):

spud = (1.3399)[o, point 0.25 of bbox dots] ..    
       (1.7087)[o, point 0.75 of bbox dots] .. 
       (1.4047)[o, point 1.25 of bbox dots] .. 
       (1.4849)[o, point 1.75 of bbox dots] .. 
       (1.5348)[o, point 2.25 of bbox dots] .. 
       (1.3187)[o, point 2.75 of bbox dots] .. 
       (1.7404)[o, point 3.25 of bbox dots] .. 
       (1.3717)[o, point 3.75 of bbox dots] .. cycle;

The way the mediation syntax works is that if you put 1/2[z0, z1] you will get a point exactly 1/2 way between z0 and z1, if you put 3/4[z0, z1] the point will be 3/4 of the way from z0 to z1, and so on. But if the fraction is greater than 1 the point will be beyond z1, so 1.5[z0, z1] will be "50%" beyond z1 on the line through z0 and z1, so since o is in the middle of the dots, each of the points in the definition of the path will make a point beyond the bbox, which will look something like this:

enter image description here

where the red box is the bbox of the dots and each red arrow points at one of the points on the spud path. So the point at the lower left is 33.99% "beyond" point 0.25 of the bounding box, and so on. The neat thing is to avoid the corners. If you can't see this then try experimenting with the start value of the loop and observe what happens.

Thruston
  • 42,268