Draw Realistic 3D crystal structure of Diamond using Tikz

Question

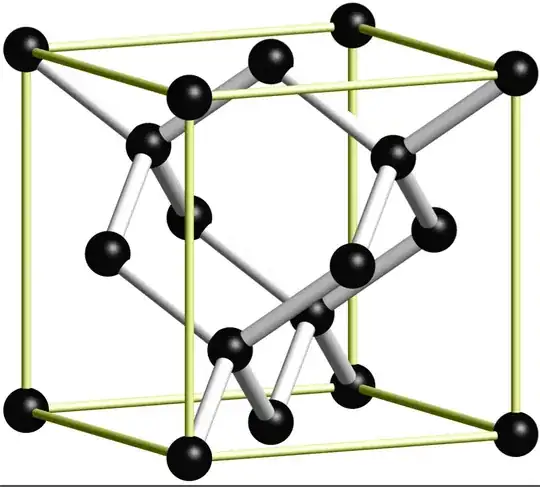
Can I draw this same exact picture(from Draw realistic 3D crystal structures (diamond)) using tikz in latex?

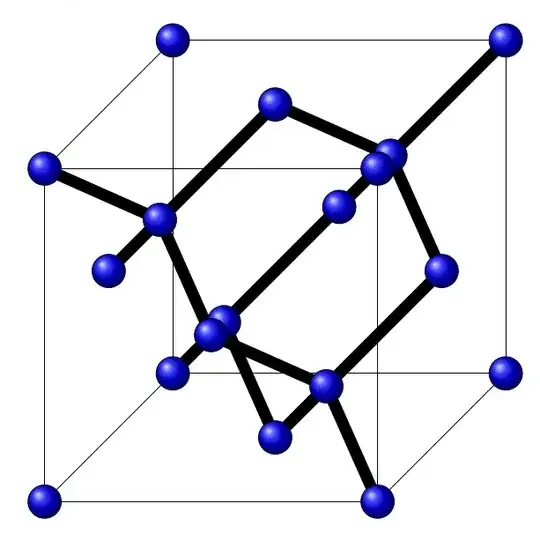
This is what I got till now.

from the code:

    \begin{tikzpicture}
    \tdplotsetmaincoords{0}{60}{140}    
    \pgfmathsetmacro{\d}{2.5}
    \draw[] (0,0,0) -- (4*\d,0,0) -- (4*\d,4*\d,0) -- (0,4*\d,0) -- (0,0,0);
    \draw[] (0,0,4*\d) -- (4*\d,0,4*\d) -- (4*\d,4*\d,4*\d) -- (0,4*\d,4*\d) -- (0,0,4*\d);
    \draw[] (0,0,4*\d) -- (4*\d,0,4*\d) -- (4*\d,0,0) -- (0,0,0) -- (0,0,4*\d);
    \draw[] (0,4*\d,4*\d) -- (4*\d,4*\d,4*\d) -- (4*\d,4*\d,0) -- (0,4*\d,0) -- (0,4*\d,4*\d);
\coordinate (Aa) at (0,0,0); 
\coordinate (Ab) at (4*\d,0,0); 
\coordinate (Ac) at (0,4*\d,0);
\coordinate (Ad) at (4*\d,4*\d,0);   
\coordinate (Ae) at  (2*\d,2*\d,0);
\coordinate (Ba) at  (\d,\d,\d);
\coordinate (Bb) at  (3*\d,3*\d,\d);        
\coordinate (Ca) at  (2*\d,0,2*\d);
\coordinate (Cb) at  (0,2*\d,2*\d); 
\coordinate (Cc) at (4*\d,2*\d,2*\d);   
\coordinate (Cd) at  (2*\d,4*\d,2*\d);
\coordinate (Da) at  (3*\d,\d,3*\d);
\coordinate (Db) at  (\d,3*\d,3*\d);
\coordinate (Ea) at  (0,0,4*\d);
\coordinate (Eb) at  (4*\d,0,4*\d);
\coordinate (Ec) at  (0,4*\d,4*\d);
\coordinate (Ed) at  (4*\d,4*\d,4*\d);
\coordinate (Ee) at  (2*\d,2*\d,4*\d);

\begin{scope}[line width=10,shade,shading angle=30]
    \draw[] (Ba) -- (Aa);
    \draw[] (Ba) -- (Ae);
    \draw[] (Bb) -- (Ae);
    \draw[] (Bb) -- (Ad);
    \draw[] (Ba) -- (Ca);
    \draw[] (Bb) -- (Cc);
    \draw[] (Bb) -- (Cd);
    \draw[] (Da) -- (Ca);
    \draw[] (Da) -- (Cc);
    \draw[] (Db) -- (Cb);
    \draw[] (Db) -- (Cd);
    \draw[] (Da) -- (Eb);
    \draw[] (Da) -- (Ee);
    \draw[] (Db) -- (Ee);
    \draw[] (Db) -- (Ec);
\end{scope}
\node[draw,circle,minimum size=1cm,shading=ball] at (Aa) {}; 
\node[draw,circle,minimum size=1cm,shading=ball] at (Ab) {}; 
\node[draw,circle,minimum size=1cm,shading=ball] at (Ac) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Ad) {};

\node[draw,circle,minimum size=1cm,shading=ball] at (Ae) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Ba) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Bb) {};

\node[draw,circle,minimum size=1cm,shading=ball] at (Ca) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Cb) {};

\node[draw,circle,minimum size=1cm,shading=ball] at (Cc) {};

\node[draw,circle,minimum size=1cm,shading=ball] at (Cd) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Da) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Db) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Ea) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Eb) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Ec) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Ed) {};
\node[draw,circle,minimum size=1cm,shading=ball] at (Ee) {};
\end{tikzpicture}

This might get you started: https://tex.stackexchange.com/a/282491/36296 — samcarter_is_at_topanswers.xyz, Aug 24 '22 at 13:57
This might also be helpful: https://tex.stackexchange.com/a/205442/36296 — samcarter_is_at_topanswers.xyz, Aug 24 '22 at 13:58
You need to show what you have tried. Also give a list of 3D coordinates of the atoms within the unit cell, so that helping people at least do not need to find them. — hpekristiansen, Aug 24 '22 at 14:02
Why don't you use LaTeX's \includegraphic to include pdf figure generated by Asymptote code in here https://tex.stackexchange.com/a/155242/140722 ? — Black Mild, Aug 25 '22 at 04:00
This is a very hard question to answer. TikZ works in 2D unlike asymptote that works in 3D. When you do \coordinate (Aa) at (0,0,0);, the 3D tuple is calculated into 2D screen coordinates and that is what is stored in (Aa). -so all information about where (Aa) really is in 3D is lost. To create a connecting rod one would like to draw it from ball surface to ball surface, instead of from center to center. -but these informations are lost. — hpekristiansen, Aug 25 '22 at 13:12
All that said, it is possible to select a projection angle and then just draw everything in 2D, but it would be a lot of manual work and it would no longer be possible to rotate the figure in 3D. — hpekristiansen, Aug 25 '22 at 13:13
To shade the rods in your code, you need to make them into filled areas - you can not do it with lines. — hpekristiansen, Aug 25 '22 at 13:14
No - as I see it, it is the same problem. tikz-3d is still just TikZ. It can help with many 3D coordinate transformation. -but is does not solve the problem with surfaces in 3d, the z-buffer problem and the loss of the 3D coordinate informations. Maybe someone mere experienced than me can figure out a way to fake it all by e.g. by calculating the order in which 2D figures needs to be drawn and how they need to look like. — hpekristiansen, Aug 25 '22 at 13:34
We can draw cylinders with endpoints on sphere but how to achieve the shade using tikz. — Akhil Akkapelli, Aug 25 '22 at 14:48

score 1 · Answer 1 · answered Aug 25 '22 at 23:41

A solution with sketch of Gene Ressler. The output of the following sketch code is a tikz code of 5542 lines.

special|\tikzstyle{BondStyle}=[thin,double=lightgray,double distance=5pt]
\tikzstyle{BordCellStyle}=[line width=6pt,lightgray!50!yellow,line cap=round]
\tikzstyle{AtomStyle}=[fill opacity=0,draw opacity=0]
|[lay=under]
def d 2.5
def O (0,0,0)
def Aa [0,0,0]
def Ab [4*d,0,0]
def Ac [0,4*d,0]
def Ad [4d,4d,0]
def Ae [2d,2d,0]
def Ba [d,d,d]
def Bb [3d,3d,d]
def Ca [2d,0,2d]
def Cb [0,2d,2d]
def Cc [4d,2d,2*d]
def Cd [2d,4d,2*d]
def Da [3d,d,3d]
def Db [d,3d,3d]
def Ea [0,0,4*d]
def Eb [4d,0,4d]
def Ec [0,4d,4d]
def Ed [4d,4d,4*d]
def Ee [2d,2d,4*d]
def pAa [Aa]+(O)
def pAb [Ab]+(O)
def pAc [Ac]+(O)
def pAd [Ad]+(O)
def pAe [Ae]+(O)
def pBa [Ba]+(O)
def pBb [Bb]+(O)
def pCa [Ca]+(O)
def pCb [Cb]+(O)
def pCc [Cc]+(O)
def pCd [Cd]+(O)
def pDa [Da]+(O)
def pDb [Db]+(O)
def pEa [Ea]+(O)
def pEb [Eb]+(O)
def pEc [Ec]+(O)
def pEd [Ed]+(O)
def pEe [Ee]+(O)
def tras rotate(10,[0,1,0]) then rotate(23,[1,0,0])
def bondstyle [line style=BondStyle]
def cellstyle [line style=BordCellStyle]
def rC 0.5
def atom {sweep[fill style=AtomStyle]{60,rotate(360/60,[0,0,1])} 
sweep{10,rotate(180/10,[1,0,0])}(0,0,-rC)}
def ret {
line[bondstyle] (pAa)(pBa)
line[bondstyle] (pAe)(pBa)
line[bondstyle] (pAe)(pBb)
line[bondstyle] (pAd)(pBb)
line[bondstyle] (pCa)(pBa)
line[bondstyle] (pCc)(pBb)
line[bondstyle] (pCd)(pBb)
line[bondstyle] (pDa)(pCa)
line[bondstyle] (pDa)(pCc)
line[bondstyle] (pDb)(pCb)
line[bondstyle] (pDb)(pCd)
line[bondstyle] (pEb)(pDa)
line[bondstyle] (pEc)(pDb)
line[bondstyle] (pEe)(pDa)
line[bondstyle] (pEe)(pDb)
line[cellstyle] (pAa)(pAb)
line[cellstyle] (pAb)(pAd)
line[cellstyle] (pAc)(pAd)
line[cellstyle] (pAa)(pAc)
line[cellstyle] (pAa)(pEa)
line[cellstyle] (pAb)(pEb)
line[cellstyle] (pAc)(pEc)
line[cellstyle] (pAd)(pEd)
line[cellstyle] (pEa)(pEb)
line[cellstyle] (pEb)(pEd)
line[cellstyle] (pEc)(pEd)
line[cellstyle] (pEa)(pEc)
put{translate([Aa])}{atom}
put{translate([Ab])}{atom}
put{translate([Ac])}{atom}
put{translate([Ad])}{atom}
put{translate([Ae])}{atom}
put{translate([Ba])}{atom}
put{translate([Bb])}{atom}
put{translate([Ca])}{atom}
put{translate([Cb])}{atom}
put{translate([Cc])}{atom}
put{translate([Cd])}{atom}
put{translate([Da])}{atom}
put{translate([Db])}{atom}
put{translate([Ea])}{atom}
put{translate([Eb])}{atom}
put{translate([Ec])}{atom}
put{translate([Ed])}{atom}
put{translate([Ee])}{atom}
}
def npAa [[tras]].(pAa)
def npAb [[tras]].(pAb)
def npAc [[tras]].(pAc)
def npAd [[tras]].(pAd)
def npAe [[tras]].(pAe)
def npBa [[tras]].(pBa)
def npBb [[tras]].(pBb)
def npCa [[tras]].(pCa)
def npCb [[tras]].(pCb)
def npCc [[tras]].(pCc)
def npCd [[tras]].(pCd)
def npDa [[tras]].(pDa)
def npDb [[tras]].(pDb)
def npEa [[tras]].(pEa)
def npEb [[tras]].(pEb)
def npEc [[tras]].(pEc)
def npEd [[tras]].(pEd)
def npEe [[tras]].(pEe)
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
special|
\fill[shading=ball,ball color=black] #1 circle[radius=14pt];
|lay=in
put{[[tras]]}{ret}
global { language tikz }

Compiling the tikz code you get:

Draw Realistic 3D crystal structure of Diamond using Tikz

1 Answers1