When PGF/TikZ plots a smooth curve through your coordinates it uses Bézier curves (as for all curves, including arcs, circles and ellipses). This curve needs two support points.
When you ask for a smooth or smooth cycled plot, these support points are calculated from the previous and the next points, the manual states:
In order to determine the control points of the curve at the point y, the handler computes the vector z − x and scales it by the tension factor (see below). Let us call the resulting vector s. Then y + s and y − s will be the control points around y.
For the smooth cycle plot the last coordinate will be the previous point for the first point and the first point will be the next point for the last point. However, for smooth the manual says:
The first control point at the beginning of the curve will be the beginning itself, once more; likewise the last control point is the end itself.
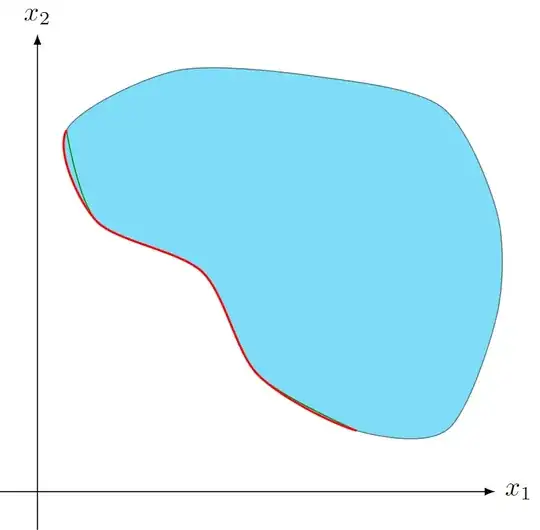
This is why your smooth plot is not equal to your closed plot on the first and last segment. It's missing the information about the very first previous and the very last next point.
With the decorations.pathreplacing library we can even inspect the the support points:

We need the red X that's on (0.38, 4.74) to be on the blue X left below of it to draw the same curve:

For this, I propose a slightly altered plothandler that uses the first and the last point to calculate the support points but does not draw any lines or curves to these points.
For this, I declare a plothandler \pgfplothandlercurvetostartend. In TikZ, this is mapped to the key smooth start and end.
You only need to supply the points to the plot yourself:
\draw[red,thick]
plot [smooth start and end, tension=0.5]
coordinates {
(1.82,5.52) % coordinate before first
(0.38,4.74) (0.78,3.54) (2.16,2.88) (2.88,1.54) (4.18,0.8)
(5.38,0.82) % coordinate after last
};
Code
\documentclass[tikz]{standalone}
\makeatletter
\tikzset{smooth start and end/.code={%
\let\tikz@plot@handler=\pgfplothandlercurvetostartend}}
\pgfdeclareplothandler{\pgfplothandlercurvetostartend}{}{
point macro=\pgf@plot@curvetostartend@handler@initial,
jump macro=\pgf@plot@smoothstartend@next@moveto}
\def\pgf@plot@smoothstartend@next@moveto{%
\global\pgf@plot@startedfalse
\global\let\pgf@plotstreampoint\pgf@plot@curvetostartend@handler@initial}
\def\pgf@plot@curvetostartend@handler@initial#1{%
\pgf@process{#1}%
\xdef\pgf@plot@curveto@first{\noexpand\pgfqpoint{\the\pgf@x}{\the\pgf@y}}%
\global\let\pgf@plot@curveto@first@support=\pgf@plot@curveto@first
\global\let\pgf@plotstreampoint=\pgf@plot@curvetostartend@handler@second}
\def\pgf@plot@curvetostartend@handler@second#1{%
\pgf@process{#1}%
\xdef\pgf@plot@curveto@second{\noexpand\pgfqpoint{\the\pgf@x}{\the\pgf@y}}%
\pgf@plot@first@action{\pgf@plot@curveto@second}%
\global\let\pgf@plotstreampoint=\pgf@plot@curvetostartend@handler@third}
\def\pgf@plot@curvetostartend@handler@third#1{%
\pgf@process{#1}%
\xdef\pgf@plot@curveto@current{\noexpand\pgfqpoint{\the\pgf@x}{\the\pgf@y}}%
% compute difference vector:
\pgf@xa=\pgf@x
\pgf@ya=\pgf@y
\pgf@process{\pgf@plot@curveto@first}%
\advance\pgf@xa by-\pgf@x
\advance\pgf@ya by-\pgf@y
% compute support directions:
\pgf@xa=\pgf@plottension\pgf@xa
\pgf@ya=\pgf@plottension\pgf@ya
% first marshal:
\pgf@process{\pgf@plot@curveto@second}%
\pgf@xb=\pgf@x
\pgf@yb=\pgf@y
\pgf@xc=\pgf@x
\pgf@yc=\pgf@y
\advance\pgf@xb by-\pgf@xa
\advance\pgf@yb by-\pgf@ya
\advance\pgf@xc by\pgf@xa
\advance\pgf@yc by\pgf@ya
\ifpgf@plot@started
\edef\pgf@marshal{\noexpand\pgfpathcurveto{\noexpand\pgf@plot@curveto@first@support}%
{\noexpand\pgfqpoint{\the\pgf@xb}{\the\pgf@yb}}{\noexpand\pgf@plot@curveto@second}}%
{\pgf@marshal}%
\else
% we didn't start yet, skip this drawing
\global\pgf@plot@startedtrue
\fi
% Prepare next:
\global\let\pgf@plot@curveto@first=\pgf@plot@curveto@second
\global\let\pgf@plot@curveto@second=\pgf@plot@curveto@current
\xdef\pgf@plot@curveto@first@support{\noexpand\pgfqpoint{\the\pgf@xc}{\the\pgf@yc}}}
\makeatother
\begin{document}
\begin{tikzpicture}
\draw[-latex] (-0.5,0) -- (6,0) node[right]{$x_1$};
\draw[-latex] (0,-0.5) -- (0,6) node[above]{$x_2$};
\draw[fill=cyan, opacity=0.5]
plot [smooth cycle,tension=0.5]
coordinates {(0.38,4.74) (0.78,3.54) (2.16,2.88) (2.88,1.54) (4.18,0.8)
(5.38,0.82) (6.02,2.32) (6.02,3.66) (5.3,5.04) (3.68,5.44) (1.82,5.52)};
% that's the wrong one
\draw[green!50!black,thin]
plot [smooth, tension=0.5]
coordinates {(0.38,4.74) (0.78,3.54) (2.16,2.88) (2.88,1.54) (4.18,0.8)};
% different plothandler and coordinate before first and coordinate after last supplied
\draw[red,thick]
plot [smooth start and end, tension=0.5]
coordinates {
(1.82,5.52) % coordinate before first
(0.38,4.74) (0.78,3.54) (2.16,2.88) (2.88,1.54) (4.18,0.8)
(5.38,0.82) % coordinate after last
};
\end{tikzpicture}
\end{document}
Output











smoothoption that does not provide the same curve when you only draw a part of the first one. Ignasi's answer is correct and seems to be the only way to do this. – SebGlav Sep 07 '22 at 15:51