Drawing with 2 parameters

Question

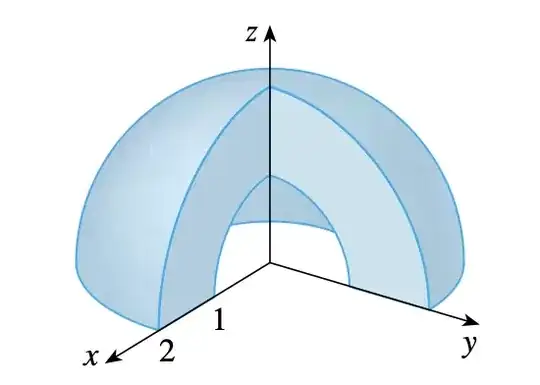
Some days ago I posted this. The code suggested really helped me to draw some nice curves and surfaces just like I wanted, but when it came to surfaces that depended on two variables/parameters I couldn't get the code to work. For example, I'm trying to do something like this

and so I started trying to plot just the surface of one sphere. I read a lot of topics on this and it always seems to use some parameter definition using pgf, but I found a code using just TikZ that I kinda liked and tried adapting to my use case.

\begin{tikzpicture}[x={(-1.3cm,-1.3cm)},y={(2.7cm,-.3cm)},z={(0cm,2cm)}, scale=0.3, > = Straight Barb]
  \draw[->] (0,0,0) -- (4,0,0) node[left] {$x$};
  \draw[->] (0,0,0) -- (0,4,0) node[below] {$y$};
  \draw[->] (0,0,0) -- (0,0,4) node[left] {$z$};
  \foreach \x/\y in {0/0, 1/1, ..., 10/10}
{
  \draw[->, ultra thick, red] ({\x}, {\y}, {(1 - {\x}**2 - {\y}**2)**(1/2)}) ;
}
\end{tikzpicture}

I put some random values for the variables just to test, but it's returning me an error

Missing number, treated as zero

I've tried changing ({\x}, {\y}, {(1 - {\x}**2 - {\y}**2)**(1/2)}) to ({\x}, {\y}, {(1 - \x**2 - \y**2)**(1/2)}) but I couldn't get rid of the error. Then I started thinking of doing something with pgf using another coordinate system, but I'm really stuck and don't know what to do and I came again to ask for help. If anyone can explain how I would get something like the image I would really appreciate it!

Does the loop even work? I doubt the ... syntax can deal with /. — Qrrbrbirlbel, Sep 12 '22 at 18:41
@Qrrbrbirlbel I got that from another question I saw on this topic so I suppose it works — tulio, Sep 12 '22 at 18:49
it can't really work, what would you expect 0/0,...,5/9 to do? also please post a test document not just a fragment — David Carlisle, Sep 12 '22 at 18:57
If you're talking about my question, I specifically said it doesn't work .. — Torbjørn T., Sep 12 '22 at 19:09

score 3 · Accepted Answer · answered Sep 12 '22 at 19:11

It's easy to draw spheres using isometric perspective. For example, with the isometric view form perspective TikZ library. With that and 3d library for the canvas is... options yo con draw something like this:

\documentclass[tikz,border=5mm]{standalone}
\usetikzlibrary{3d,perspective}
\tikzset
{
  axis/.style={black,-latex},
  xy/.style={canvas is xy plane at z=0},
  xz/.style={canvas is xz plane at y=0},
  yz/.style={canvas is yz plane at x=0},
}
\begin{document}

\begin{tikzpicture}[line cap=round,line join=round,isometric view,rotate around z=180,blue]
  % sphere, inside
  \draw[xy,fill=blue!60] (2,0) arc (0:-270:2) -- (0,1) arc (90:360:1) -- cycle;
  % sphere, outside
  \draw[shading=ball,ball color=blue!60] 
        {[xy] (2,0) arc (0:-45:2)} arc (180:0:2 cm) 
        {[xy] arc (135:90:2)} -- (0,0,2) -- cycle;
  % slices
  \draw  [xz,fill=blue!20] (1,0) -- (2,0) arc (0:90:2) -- (0,1) arc (90:0:1) -- cycle;
  \draw  [yz,fill=blue!30] (1,0) -- (2,0) arc (0:90:2) -- (0,1) arc (90:0:1) -- cycle;
  % axes
  \draw[axis] (0,0,0) -- (3,0,0) node[left]  {\strut$x$};
  \draw[axis] (0,0,0) -- (0,3,0) node[right] {\strut$y$};
  \draw[axis] (0,0,0) -- (0,0,3) node[above] {$z$};
\end{tikzpicture}
\end{document}

@TulioAlves, a paraboloid wont be so easy but it can be done. Perhaps pgfplots or asymptote could be a better tool in this case. However, take a look at this post: https://tex.stackexchange.com/questions/619390/how-can-i-draw-the-surface-fx-y-x2y2-like-my-picture/619495 — Juan Castaño, Sep 13 '22 at 06:09

Drawing with 2 parameters

1 Answers1