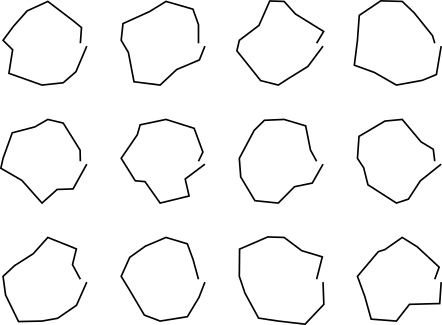
Interesting!
Here are three workarounds …
Only decorate the circle and close the path yourself.
\tikz
\foreach \x in {0,1,2,3}
\foreach \y in {0,1,2}
\draw [decoration={random steps, segment length=4pt}]
(\x,\y) decorate {circle[radius=.3cm]} -- cycle;
Use a very small post length and post=lineto (it doesn't really close the path but at least the line ends where it started):
\tikz
\foreach \x in {0,1,2,3}
\foreach \y in {0,1,2}
\draw [decorate, decoration={
random steps, segment length=4pt, post length=0.01pt, post=lineto
}] (\x,\y) circle[radius=.3cm];
As 2. but uses a close decoration at its post:
\pgfdeclaredecoration{close}{initial}{%
\state{initial}[width=\pgfdecoratedremainingdistance]{\pgfpathclose}%
\state{final}{}}%
% …
\tikz
\foreach \x in {0,1,2,3}
\foreach \y in {0,1,2}
\draw [decorate, decoration={
random steps, segment length=4pt, post length=0.01pt, post=close
}] (\x,\y) circle[radius=.3cm];
… and a totally different approach:
\tikz
\foreach \xxx in {0,1,2,3}
\foreach \yyy in {0,1,2}
\draw plot [
sharp cycle,
samples at = {0,...,9},
shift={(\xxx,\yyy)}
] (360*\x/10+rnd*30:.3cm+.1cm*rnd);
Of course one can play with all the different values to get different kinds of “circles”.
The sharp cycle key (that is missing from the manual) makes sure that the path is closed again.
Code
\documentclass[tikz]{standalone}
\usetikzlibrary{decorations.pathmorphing}
\pgfdeclaredecoration{close}{initial}{%
\state{initial}[width=\pgfdecoratedremainingdistance]{\pgfpathclose}%
\state{final}{}}%
\begin{document}
\tikz
\foreach \x in {0,1,2,3}
\foreach \y in {0,1,2}
\draw [decoration={random steps, segment length=4pt}]
(\x,\y) decorate {circle[radius=.3cm]} -- cycle;
\tikz
\foreach \x in {0,1,2,3}
\foreach \y in {0,1,2}
\draw [decorate, decoration={
random steps, segment length=4pt, post length=0.01pt, post=lineto
}] (\x,\y) circle[radius=.3cm];
\tikz
\foreach \x in {0,1,2,3}
\foreach \y in {0,1,2}
\draw [decorate, decoration={
random steps, segment length=4pt, post length=0.01pt, post=close
}] (\x,\y) circle[radius=.3cm];
\tikz
\foreach \xxx in {0,1,2,3}
\foreach \yyy in {0,1,2}
\draw plot [
sharp cycle,
samples at = {0,...,9},
shift={(\xxx,\yyy)}
] (360\x/10+rnd30:.3cm+.1cm*rnd);
\end{document}
Output (last example)