No, but you can do
\NewDocumentCommand{\com}{mo}{%
\operatorname{com}(#1,\IfNoValueTF{#2}{r_{#1}}{#2})%
}
and call either
\com{x}
or
\com{x}[y]
If r_ should be used in either case, the definition can be even simpler
\NewDocumentCommand{\com}{mO{#1}}{%
\operatorname{com}(#1,r_{#2})%
}
Actually, it is possible. It's up to you if you want to break all syntax conventions of LaTeX and be prepared to get weird output now and then.
\documentclass{article}
\usepackage{amsmath}
\ExplSyntaxOn
\NewDocumentCommand{\com}{}
{
\peek_regex_replace_once:nn
{ ( { [^\}]* } )* } % search all braced groups
{ \c{lorenzo_com:n} {\0} } % pass them as single argument to \lorenzo_com:n
}
\cs_new_protected:Nn \lorenzo_com:n
{
\operatorname{com}
\int_case:nnF { \tl_count:n { #1 } }
{
{0}{}
{1}{__lorenzo_com:n #1}
}
{__lorenzo_com:nn #1}
}
\cs_new_protected:Nn __lorenzo_com:n { (#1,r\sb{#1}) }
\cs_new_protected:Nn __lorenzo_com:nn { (#1,#2) }
\ExplSyntaxOff
\begin{document}
$\com{x}+y$
$\com{x}{y}+z$
$\com{x} {y}+z$
$\com{x}{y}{z}+u$
\end{document}
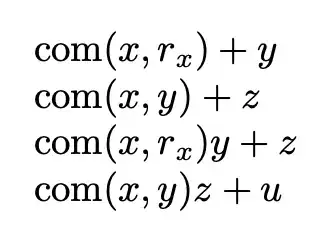
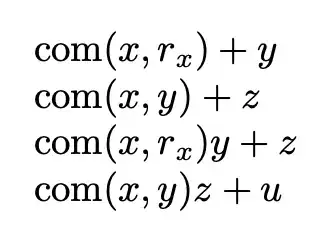
[]not{}so\com{x}and\com[i][x}– David Carlisle Dec 29 '22 at 19:16\com{x}and\com{x}{y}, or\com(x)and\com(x)(y)or\com[x]and\com[x][y]? Or would a mixture\com{x}and\com[x]{y}suffice? – Werner Dec 29 '22 at 19:39