How to get the last circle behind the first one?

Question

As the question says, how to get the last circle behind the first one in the following picture?
The MWE is

\documentclass{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
  \def\n{20}
  \def\a{360/\n}
  \foreach \i in {1,...,\n}{
    \draw[fill=yellow] (\i*\a:2) circle [radius=1];
  }
\end{tikzpicture}
\end{document}

I do not know how to do it in tikz, but you can instead of filling and drawing the circles create a path that consists of the little piece you want to have, and draw it. In this image I made the little piece green. In MetaPost (that I used) the piece is simply made by using buildcycle, but as mentioned, I do not know how to do it in tikz. But I'm sure someone else will help with that. — mickep, Jan 01 '23 at 10:44
Use a clip probably. Related: tikz pgf - Modifying \foreach loop to make first loop overlaps last one - TeX - LaTeX Stack Exchange — user202729, Jan 01 '23 at 10:48

Juan Castaño · Answer 1 · 2023-01-02T13:29:03.873

UPDATE: This is a more configurable solution, and easier in the maths department too.

For this one I made two \pics, one for the 'petals' and another for the 'flower' that repeats and rotate the petals.

Like this:

\documentclass[tikz,border=2mm]{standalone}
\tikzset
{
  pics/petal/.style 2 args={% #1 = radius, #2 = distance to the next petal
    code={
      \pgfmathsetmacro\half{0.5*#2}
      \ifdim\half pt<#1 pt % if the petals intersect
        \pgfmathsetmacro\aa{acos(\half/#1)}
        \path[pic actions] (\aa:#1) arc (\aa:360-\aa:#1) arc (180+\aa:180-\aa:#1);
      \else % if the petals don't intersect
        \draw[pic actions] (0,0) circle [radius=#1];
      \fi
    }},
  pics/flower/.style n args={3}{% #1 = flower radius, #2 = petal radius, #3 = number of petals
    code={
      \pgfmathsetmacro\dd{#1*sqrt(2*(1-cos(360/#3))} % distance between petals
      \foreach\i in {1,...,#3}
        \pic[draw,fill,rotate=180/#3+360*\i/#3+90] at (360*\i/#3:#1) {petal={#2}{\dd}};
    }},
}
\begin{document}
\begin{tikzpicture}[line cap=round,line join=round]
\foreach\i in {1,...,4}
  \pic[fill=green!20,rotate=90\i+180] at (90\i:4) {petal={1}{1}};
\pic[draw=red ,fill=red!20]  {flower={3}{1}{12}};
\pic[draw=blue,fill=blue!10] {flower={3}{0.2}{4}};
\pic[draw=blue,fill=blue!30] {flower={1}{0.2}{20}};
\foreach\i in {1,...,12}
  \pic[fill=yellow,rotate=30\i] at (30\i:3) {flower={0.4}{0.1}{7}};
\end{tikzpicture}
\end{document}

INITIAL ANSWER:

I'm creating a \pic that draws only the visible part of the circle (the same idea that mickep proposes, I think). Then I draw it and rotate each time.

It needs to compute a couple of angles using the cosine theorem (for example).

This is my solution:

\documentclass[tikz,border=2mm]{standalone}
\begin{document}
\begin{tikzpicture}
\def\n{20}
\pgfmathsetmacro\a{360/\n}
\pgfmathsetmacro\aa{acos(4cos(\a)-3)} % some other angles
\pgfmathsetmacro\bb{90-0.5\aa}        % obtained from the
\pgfmathsetmacro\cc{0.5\aa-0.5\a}    % cosine theorem
\tikzset
{% a pic (like a crescent moon)
  pics/moon/.style={
    code={
      \path[pic actions] (0:2) ++ (180-\cc:1) arc (180-\cc:540-\cc-2\bb:1) arc (\a-180+\cc+2\bb:\a-180+\cc:1);
    }},
}
\foreach \i in {1,...,\n}
  \pic[draw,fill=yellow,rotate=\a\i] (\a\i:2) {moon};
\end{tikzpicture}
\end{document}

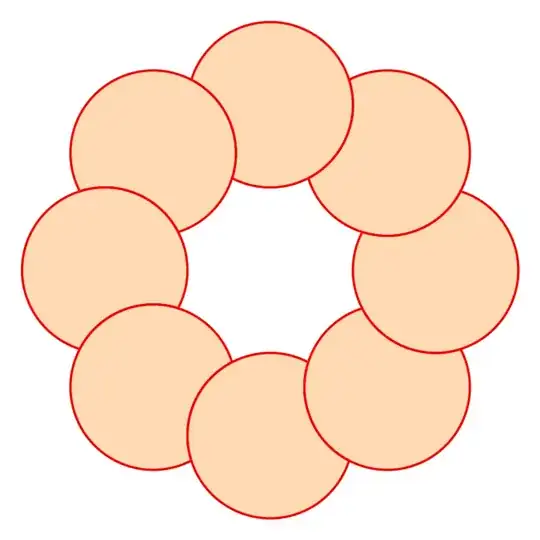
Or, changing

\def\n{8}
....
\pic[draw=red,thick,fill=orange!30,rotate=\a*\i] (\a*\i:2) {moon};
....

Yes, that is what I did (but perhaps with less manual calculations). I can add the code for what I did, it might help someone. — mickep, Jan 01 '23 at 12:38

hpekristiansen · Answer 2 · 2023-01-01T19:43:26.613

5

\documentclass[tikz, border=1cm]{standalone}
\begin{document}
\begin{tikzpicture}
\def\n{20}
\def\a{360/\n}
\foreach \i in {1,...,\n}
   \draw[fill=yellow] (\i*\a:2) circle[radius=1];
\clip (0,-3) rectangle (3,3);
\foreach \i in {1,...,\n}
   \draw[fill=yellow] ({int(\i-\n/2)*\a}:2) circle[radius=1];
\end{tikzpicture}
\end{document}

edited Jan 01 '23 at 19:43

answered Jan 01 '23 at 12:54

hpekristiansen

37,006

score 4 · Answer 3 · answered Jan 01 '23 at 12:42

Since you now how a tikz answer that works for you, here is the code that I used to draw the image in my comment:

\startMPpage[offset=1dk]
numeric N ; N := 20 ;
path c[] ;
c[1] := fullcircle rotated 180 scaled 2cm yshifted 2cm ;
c[2] := reverse c[1] rotated (360/N) ;
c[3] := buildcycle(c[1],c[2]) ;
for i = 0 upto N - 1:
  fill c[3] rotated (i360/N) withcolor yellow ;
  draw c[3] rotated (i360/N) ;
endfor
fill c[3] withcolor darkgreen ;
draw c[3] withcolor darkred ;
\stopMPpage

A few comments:

The last fill and draw of course only shows the green and red piece that is used.
The rotated 180 and reverse are there only so that buildcycle will choose the right piece.

I notice that the yellow color is different in tikz and MetaPost. That was new to me.

How to get the last circle behind the first one?

3 Answers3