Tikz: How to make the arrow bend along the curve in decoration?

Question

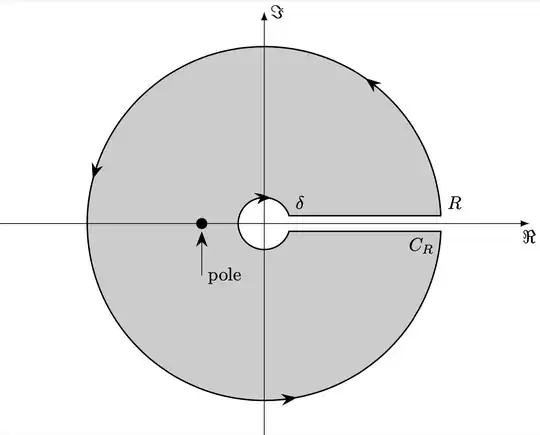
When I'm drawing a contour, I want to know how to make the arrow bend along the curve in decoration. Please see the example below.

Here is my MWE:

\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{decorations.markings}
\usetikzlibrary{arrows.meta}
\usetikzlibrary{calc}
\usetikzlibrary{bending} % Bend the arrow
\begin{document}
\begin{tikzpicture}[>={Stealth[length=0.3cm,bend]},
        decoration={markings,
        mark= at position .1 with {\arrow{>}},
        mark= at position .32 with {\arrow{>}},
        mark= at position .55 with {\arrow{>}},
        mark= at position 0.88 with {\arrow{>}}, % <----
        }
    ]
        \def\gap{0.3}
        \def\bigradius{3.4}
        \def\littleradius{0.5}
    \filldraw[postaction = {decorate}, thick ,fill=gray!40] 
    let 
        \n1 = {asin(\gap/2/\bigradius)},
        \n2 = {asin(\gap/2/\littleradius)}
    in
        (0+\n1:\bigradius) node[above right]{$R$}  arc (0+\n1:360-\n1:\bigradius) node[below left]{$C_{R}$} -- (0-\n2:\littleradius) arc (360-\n2:0+\n2:\littleradius) node[above right]{$\delta$} -- cycle;
    \fill (-1.2,0)  circle (3pt) ;
    \draw[-&gt;] (-1.2,-1) node[right]{pole} --(-1.2,-0.15);

    % axis
    \draw[-Latex] (-1.5*\bigradius,0) -- (1.5*\bigradius,0) node[below]{$\Re$} ;
    \draw[-Latex] (0,-1.2*\bigradius) -- (0,1.2*\bigradius) node[right]{$\Im$};

\end{tikzpicture}
\end{document}

As you can see, the fourth arrow on the contour looks strange. I want it to bend along the curve, that's why I want to use \usetikzlibrary{bending}. But in the decoration, it seems that the arrow cannot be bent, and the bend command cannot take effect.

I would like to ask is there any solution?

One of my solutions:

\documentclass{standalone}
\usepackage{tikz}
\usepackage{physics}
\usetikzlibrary{decorations.markings}
\usetikzlibrary{arrows.meta}
\usetikzlibrary{calc}
\usetikzlibrary{bending}% Bend the arrow
\begin{document}
\begin{tikzpicture}[>={Stealth[length=0.3cm,bend]},
        decoration={markings,
        mark= at position .1 with {\arrow{>}},
        mark= at position .32 with {\arrow{>}},
        mark= at position .55 with {\arrow{>}},
        % mark= at position 0.88 with {\arrow{>}},
        }
    ]
        \def\gap{0.3}
        \def\bigradius{3.4}
        \def\littleradius{0.5}
    \filldraw[postaction = {decorate}, thick ,fill=gray!40] 
    let 
        \n1 = {asin(\gap/2/\bigradius)},
        \n2 = {asin(\gap/2/\littleradius)}
    in
        (0+\n1:\bigradius) node[above right]{$R$}  arc (0+\n1:360-\n1:\bigradius) node[below left]{$C_{R}$} -- (0-\n2:\littleradius) arc (360-\n2:0+\n2:\littleradius) node[above right]{$\delta$} -- cycle;
    % draw an arrow alone
    \draw[thick,->] (300:\littleradius) arc (300:130:\littleradius) node[above]{$C_{\delta}$};

    \fill (-1.2,0)  circle (3pt) ;
    \draw[->] (-1.2,-1) node[right]{pole} --(-1.2,-0.15);

    % axis
    \draw[-Latex] (-1.5*\bigradius,0) -- (1.5*\bigradius,0) node[below]{$\Re$} ;
    \draw[-Latex] (0,-1.2*\bigradius) -- (0,1.2*\bigradius) node[right]{$\Im$};

\end{tikzpicture}
\end{document}

Answer 1

Purely for comparison, here is a version in Metapost. The default arrowheads in MP always follow the curve of the path. This is more noticeable on the inner ring.

This is wrapped up in luamplib so you need to compile it with lualatex.

\documentclass[border=5mm]{standalone}
\usepackage{luamplib}
\begin{document}
\mplibtextextlabel{enable}
\begin{mplibcode}
beginfig(1);
% some control values
numeric delta, R, gap;
delta = 13; R = 89; gap = 3;
% axes and the region to fill
path re, im, region, little_ring, big_ring;
re = (left -- right) scaled 5/4 R;
im = re rotated 90;
little_ring = reverse fullcircle scaled 2 delta
         cutbefore subpath (1/2, 1) of re shifted (0, -gap)
         cutafter  subpath (1/2, 1) of re shifted (0, +gap);
big_ring = fullcircle scaled 2 R
         cutbefore subpath (1/2, 1) of re shifted (0, +gap)
         cutafter  subpath (1/2, 1) of re shifted (0, -gap);
region = little_ring -- big_ring -- cycle;
% do the filling first so it is on the bottom
% grey scale is just a single number between 0 and 1
fill region withcolor 7/8;
% use narrower arrowheads
ahangle := 36;
% draw the axes and the pole marker, with fine pen
drawoptions(withpen pencircle scaled 1/4);
drawarrow re;
drawarrow im;
z1 = (-3 delta, 0); z2 = z1 shifted 16 down;
draw z1 withpen pencircle scaled dotlabeldiam;
drawarrow z2 -- z1 cutafter fullcircle scaled 6 shifted z1;
drawoptions();
% bigger arrowheads for the integral path
ahlength := 6;
drawarrow subpath (0, 5) of region;
drawarrow subpath (5, 10) of region;
drawarrow subpath (10, 12.5) of region;
drawarrow subpath (12.5, 15.5) of region;
draw      subpath (15.5, 18) of region;
% add the labels
label.bot("Pole", z2);
label.rt("$\Re$", point 1 of re);
label.top("$\Im$", point 1 of im);
label.urt("$\delta$", point 8 of little_ring);
label.urt("$R$", point 0 of big_ring);
label.ulft("$C_\delta$", point 5.3 of little_ring);
label.ulft("$C_R$", point 7.6 of big_ring);
endfig;
\end{mplibcode}
\end{document}

Answer 2

The hobby library allows one to draw a smooth curve through a given set of points. With the markings library one can record a number of points along the path that one decorate, and then draw a bent arrow through those points. This is what the bent arrow at style below does. In its current form it hard codes the distance of the points that the length of the curve matches the length of the arrow in your example.

\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{decorations.markings}
\usetikzlibrary{arrows.meta}
\usetikzlibrary{calc}
\usetikzlibrary{bending} % Bend the arrow
\usetikzlibrary{hobby}% smooth curve through a set of given points
\begin{document}
\begin{tikzpicture}[>={Stealth[length=0.3cm,bend]},
        bent arrow at/.style={decoration={markings,
            mark=at position {#1\pgfdecoratedpathlength-0.15cm} with {\coordinate (bent arrow 1);},
            mark=at position {#1\pgfdecoratedpathlength-0.05cm} with {\coordinate (bent arrow 2);},
            mark=at position {#1\pgfdecoratedpathlength+0.05cm} with {\coordinate (bent arrow 3);},
            mark=at position {#1\pgfdecoratedpathlength+0.15cm} with {\coordinate (bent arrow 4);
            \draw[-{Stealth[length=0.3cm,bend]}] (bent arrow 1) to[curve through={(bent arrow 2) .. (bent arrow 3)}]  (bent arrow 4) ;}
        }}
    ]
        \def\gap{0.3}
        \def\bigradius{3.4}
        \def\littleradius{0.5}
    \filldraw[postaction = {bent arrow at/.list={.1,.32,.55,.88},decorate}, thick ,fill=gray!40] 
    let 
        \n1 = {asin(\gap/2/\bigradius)},
        \n2 = {asin(\gap/2/\littleradius)}
    in
        (0+\n1:\bigradius) node[above right]{$R$}  arc (0+\n1:360-\n1:\bigradius) node[below left]{$C_{R}$} -- (0-\n2:\littleradius) arc (360-\n2:0+\n2:\littleradius) node[above right]{$\delta$} -- cycle;
    \fill (-1.2,0)  circle (3pt) ;
    \draw[->] (-1.2,-1) node[right]{pole} --(-1.2,-0.15);

    % axis
    \draw[-Latex] (-1.5*\bigradius,0) -- (1.5*\bigradius,0) node[below]{$\Re$} ;
    \draw[-Latex] (0,-1.2*\bigradius) -- (0,1.2*\bigradius) node[right]{$\Im$};

\end{tikzpicture}
\end{document}