factorizing quadratic equations with expl3

Question

My goal is to illustrate the "completing the square" technique for factorizing quadratic equations. I'd like code that could handle a wide range of coefficients, including integers, some support for rationals, and numeric values. I'm very new to the expl3 syntax and have attempted to adapt code found here and here. But I'm missing some basic things.

In the experimental code below, the case of the rational -3/2 is not handled properly, with the sign in the denominator. I'd also like to suppress unit coefficients like 1x. Ultimately, I would like to order the roots and to replace $(x+1)(x+1)$ with $(x+1)^2$. Any general coding tip welcome too! Thanks.

\documentclass[10pt,t]{beamer}
\geometry{paperwidth=160mm,paperheight=96mm}% aspectratio=169: 160mm x 90mm
\usefonttheme{professionalfonts}%
\setbeamertemplate{navigation symbols}{}% nobody likes you
\usepackage{xfp}% math calculations
\usepackage{xparse}
% https://tex.stackexchange.com/questions/480444
\ExplSyntaxOn
% reduce reducible fractions
% https://tex.stackexchange.com/questions/253693
\cs_new:Nn \svend_gcd:nn
  {
    \int_compare:nNnTF {#2} = { 0 } {#1}
      { \svend_gcd:ff {#2} { \int_mod:nn {#1} {#2} } }
  }
\cs_generate_variant:Nn \svend_gcd:nn { ff }
\int_new:N \l__svend_tmp_int
\cs_new:Nn \svend_reduced:nn
 {
    \int_set:Nn \l__svend_tmp_int { \svend_gcd:nn {#1} {#2} }
\fp_compare:nT 
  { #2 = \l__svend_tmp_int } 
  { \int_eval:n { #1 / \l__svend_tmp_int } }

\fp_compare:nF 
  { #2 = \l__svend_tmp_int } 
  { { \int_eval:n { #1 / \l__svend_tmp_int } }
    \over
    { \int_eval:n { #2 / \l__svend_tmp_int } }
  }

}
% Quadratic form
\NewDocumentCommand{\QuadraticForm}{O{x}mmm}
 {
  \ensuremath{
    \str_case:nnF { #2 }
     {
      {1}{}
      {-1}{-}
     }
     {#2}
     #1^{2}
    \str_case:nnF { #3 }
     {
      {0}{}
      {1}{+#1}
      {-1}{-#1}
     }
     { 
      \fp_compare:nT { #3 > 0 } { + } #3#1 
     }
    \fp_compare:nF { #4 = 0 }
     {
      \fp_compare:nT { #4 > 0 } { + }
     }
    #4
  }
}
% Quadratic roots
\cs_new:Nn \sandu_solve:nnnn
   {
    \fp_eval:n { round( ( -(#3) #1 sqrt((#3)^2-4(#2)(#4)) )/(2*(#2)), 4) }
   }
\NewDocumentCommand{\QuadraticRoots}{O{x}mmm}
 {
  \ensuremath{
    #1=\sandu_solve:nnnn{+}{#2}{#3}{#4},
    #1=\sandu_solve:nnnn{-}{#2}{#3}{#4}
  }
}
% Leading coefficient
\NewDocumentCommand{\LeadingCoeff}{O{x}mmm}
 {
  \ensuremath{#2}
}
% Linear coefficient
\NewDocumentCommand{\LinearCoeff}{O{x}mmm}
 {
  \ensuremath{#3}
}
% Constant coefficient
\NewDocumentCommand{\ConstantCoeff}{O{x}mmm}
 {
  \ensuremath{#4}
}
% Variable name
\NewDocumentCommand{\VariableName}{O{x}mmm}
 {
  \ensuremath{#1}
}
% Monic form
\NewDocumentCommand{\MonicForm}{O{x}mmm}
 {
  \ensuremath{
     #1^{2}
    \str_case:nnF { #3/#2 }
     {
      {0}{}
      {1}{+#1}
      {-1}{-#1}
     }
     { 
      \fp_compare:nT { #3/#2 > 0 } { + } { \svend_reduced:nn {#3} {#2} } #1 
     }
    \fp_compare:nF { #4 = 0 }
     { 
      \fp_compare:nT { #4/#2 > 0 } { + } { \svend_reduced:nn {#4} {#2} }
     }
  }
}
% Leading coefficient factored out
\NewDocumentCommand{\FactorLeadingCoeff}{O{x}mmm}
 { 
  \ensuremath{
    \fp_compare:nTF { #2 = 1 } { \MonicForm[#1]{#2}{#3}{#4} }{ #2 \left(\MonicForm[#1]{#2}{#3}{#4}\right) }
  }
}
% Product form
\NewDocumentCommand{\ProductForm}{O{x}mmm}
 { 
  \ensuremath{
\fp_compare:nF { \sandu_solve:nnnn{+}{#2}{#3}{#4} < 0 }
  { \left(#1 \fpeval{-\sandu_solve:nnnn{+}{#2}{#3}{#4}}\right) }
\fp_compare:nF { \sandu_solve:nnnn{-}{#2}{#3}{#4} < 0 }
  { \left(#1 \fpeval{-\sandu_solve:nnnn{-}{#2}{#3}{#4}}\right) }
\fp_compare:nF { \sandu_solve:nnnn{+}{#2}{#3}{#4} > 0 }
  { \left(#1+\fpeval{-\sandu_solve:nnnn{+}{#2}{#3}{#4}}\right) }
\fp_compare:nF { \sandu_solve:nnnn{-}{#2}{#3}{#4} > 0 }
  { \left(#1+\fpeval{-\sandu_solve:nnnn{-}{#2}{#3}{#4}}\right) }
}
}
% Factored form
\NewDocumentCommand{\FactoredForm}{O{x}mmm}
 { 
  \ensuremath{
    \fp_compare:nTF { #2 = 1 } { \ProductForm[#1]{#2}{#3}{#4} }{ #2 \ProductForm[#1]{#2}{#3}{#4} }
  }
}
\ExplSyntaxOff
\setbeamercovered{transparent=0}% remove transparency of overlays
\begin{document}
\begin{frame}[allowframebreaks]
\frametitle{Factoring Quadratic Equations}
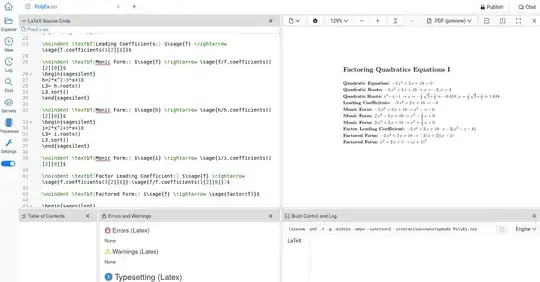
Quadratic equation: $\QuadraticForm{-3}{3}{18}=0 \quad\checkmark$
Quadratic roots: $\QuadraticForm{-3}{3}{18} \to \QuadraticRoots{-3}{3}{18} \quad\checkmark$
Quadratic roots: $\QuadraticForm{1}{-1}{-1} \to \QuadraticRoots{1}{-1}{-1} \to$ order from smaller to larger root
Leading coefficient: $\QuadraticForm{-3}{3}{18} \to \LeadingCoeff{-3}{3}{18} \quad\checkmark$
Monic form: $\QuadraticForm{-3}{3}{18} \to \MonicForm{-3}{3}{18} \to$ remove unit linear coefficient $1x$
Monic form: $\QuadraticForm{2}{-3}{18} \to \MonicForm{2}{-3}{18} \to$ fix the sign in the denominator
Monic form: $\QuadraticForm{2}{3}{18} \to \MonicForm{2}{3}{18} \quad\checkmark$
Factor leading coefficient: $\QuadraticForm{-3}{3}{18} \to \FactorLeadingCoeff{-3}{3}{18} \quad\checkmark$
Factored form: $\QuadraticForm{-3}{3}{18} \to \FactoredForm{-3}{3}{18} \quad\checkmark$
Factored form: $\QuadraticForm{1}{2}{1} \to \FactoredForm{1}{2}{1} \to$ repeated roots to be squared
\end{frame}
\end{document}

Answer 1

Here is an example of how sagetex can help solve your problem, followed by some explanation. First, the code:

\documentclass{article}
\usepackage{sagetex,amsmath}
\linespread{1.2}
\begin{document}
\noindent\textbf{\Large Factoring Quadratics Equations I}\\
\begin{sagesilent}
f=-3*x^2+3*x+18
L= f.roots()
L.sort()
\end{sagesilent}
\noindent \textbf{Quadratic Equation:} $\sage{f}=0$
\noindent \textbf{Quadratic Roots:} $\sage{f} \rightarrow x=\sage{L[0][0]}, x=\sage{L[1][0]}$
\begin{sagesilent}
g=x^2-x-1
L2= g.roots()
L2.sort()
\end{sagesilent}
\noindent \textbf{Quadratic Roots:} $\sage{g} \rightarrow x=\sage{L2[0][0]} \approx \sage{(L2[0][0]).n(digits=3)}, x=\sage{L2[1][0]} \approx \sage{(L2[1][0]).n(digits=4)}$
\noindent \textbf{Leading Coefficients:} $\sage{f} \rightarrow \sage{f.coefficients()[2][0]}$
\noindent \textbf{Monic Form:} $\sage{f} \rightarrow \sage{f/f.coefficients()[2][0]}$
\begin{sagesilent}
h=2x^2-3x+18
L3= h.roots()
L3.sort()
\end{sagesilent}
\noindent \textbf{Monic Form:} $\sage{h} \rightarrow \sage{h/h.coefficients()[2][0]}$
\begin{sagesilent}
i=2x^2+3x+18
L3= i.roots()
L3.sort()
\end{sagesilent}
\noindent \textbf{Monic Form:} $\sage{i} \rightarrow \sage{i/i.coefficients()[2][0]}$
\noindent \textbf{Factor Leading Coefficient:} $\sage{f} \rightarrow \sage{f.coefficients()[2][0]}(\sage{f/f.coefficients()[2][0]})$
\noindent \textbf{Factored Form:} $\sage{f} \rightarrow \sage{factor(f)}$
\begin{sagesilent}
j=x^2+2*x+1
\end{sagesilent}
\noindent \textbf{Factored Form:} $\sage{j} \rightarrow \sage{factor(j)}$
\end{document}

The output running in Cocalc:

Explanation: The information and calculations are done by Sage in the sagesilent blocks. This information is like scratch work: it isn't typeset by LaTeX and we grab what we need with the appropriate sagetex macro. For numeric data, \sage{} takes it from our scratch work and inserts it into LaTeX. So, for example after defining f=-3*x^2+3*x+18 as my polynomial in sagesilent the LaTeX code $\sage{f}=0$ results in the equation -3*x^2+3*x+18=0. L= f.roots() creates a list of 2-tuples (the root and its multiplicity) while L.sort() orders the roots from smallest to largest. The command x=\sage{L[0][0]} takes the smallest root (Python considers it the zeroth position in the list) and we want the root (not the multiplicity) so L[0][0]. If we wanted the multiplicity of the first root we can get it with L[0][1].

This can be better seen by going to a Sage Cell Server typing f=-3*x^2+3*x+18 on Line 1 followed by f.roots() on Line 2 and pressing enter. The documentation for learning Sage is enormous. The 700+ page documentation on Polynomials is here. To get a better overview of Sage without drowning in the details, a free book is a helpful. In this guide, page 131 has some essential Sage commands for polynomials. Notice the command for getting the coefficients of a polynomial. If I go to my Sage cell server and type as below

The output is [[18, 0], [3, 1], [-3, 2]] which tells me that 18 is the coefficient of x^0, 3 is the coefficient of x^1, and -3 is the coefficient of x^2. That's because if f=-3*x^2+18 we'd get [[18, 0], [-3, 2]]. To force all coefficients to be printed f.coefficients(sparse=False) will work. If you go to the LaTeX code: \sage{i/i.coefficients()[2][0], where i=2*x^2+3*x+18 we'd have output [[18, 0], [3, 1], [2, 2]] where i.coefficients()[2] refers to the 2-tuple [2, 2] and i.coefficients()[2][0] refers to the first 2 (in the zeroth position) of [2,2] hence \sage{i/i.coefficients()[2][0] is just 2*x^2+3*x+18 divided by 2.

In your comment you said "I'd be open to other solutions. Any reason not to use expl?". First, by working with what is built into Sage, you can solve your problems more quickly. Need to factor a polynomial (or number): easy because factor is already defined. If Sage is missing something, defining a Python function can help. Second, Sage solutions are generally shorter because a CAS has stepped in to help, such as handling +- issues. Third, it's also easier to read and remember Python. I, for one, can't figure out what's happening in your expl code. Likewise, with Sage doing the work, as opposed to someone coding from scratch the results are more likely to be correct--it's just a matter of picking up the documentation you need to code the solution. Finally, Sage is ready to help for harder problems such as polynomials of higher degree and integration, differentiation, matrices, graph theory and more. As a CAS, Sage has no problem simplifying square roots. The main drawback is Sage is not a part of LaTeX. The easiest way to access it is with a free Cocalc account. If you are more computer savy, you can download it and get it to communicate with your LaTeX distribution.