You can reproduce the picture
\documentclass{article}
\usepackage{amsmath}
\usepackage{mathptmx}
\begin{document}
[
[P(\theta)]=\sqrt{\frac{2}{3}}
\begin{bmatrix}
\cos\theta & \cos(\theta-\dfrac{2\pi}{3}) & \cos(\theta+\dfrac{2\pi}{3}) \
-\sin\theta & -\sin(\theta-\dfrac{2\pi}{3}) & -\sin(\theta+\dfrac{2\pi}{3}) \
\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}}
\end{bmatrix}
]
\end{document}

But, looking at the output, you clearly see that there are several aspects to fix:
- the parentheses are wrong, because too short;
- the first two lines touch each other;
- the symbols are too big inside the matrix.
You might fix just the first two aspects noted above. First of all with NewTX instead of mathptmx, larger parentheses and some vertical space:
\documentclass{article}
\usepackage{amsmath}
\usepackage{newtxtext,newtxmath}
\begin{document}
[
[P(\theta)]=\sqrt{\frac{2}{3}}
\begin{bmatrix}
\cos\theta & \cos\Bigl(\theta-\dfrac{2\pi}{3}\Bigr) & \cos\Bigl(\theta+\dfrac{2\pi}{3}\Bigr)
\[2ex]
-\sin\theta & -\sin\Bigl(\theta-\dfrac{2\pi}{3}\Bigr) & -\sin\Bigl(\theta+\dfrac{2\pi}{3}\Bigr)
\[1.5ex]
\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}}
\end{bmatrix}
]
\end{document}

However, I'd use smaller fractions in the first two rows and slashed fractions in the last row.
\documentclass{article}
\usepackage{amsmath}
\usepackage{newtxtext,newtxmath}
\begin{document}
[
[P(\theta)]=\sqrt{\frac{2}{3}}
\begin{bmatrix}
\cos\theta & \cos\bigl(\theta-\frac{2\pi}{3}\bigr) & \cos\bigl(\theta+\frac{2\pi}{3}\bigr)
\[1ex]
-\sin\theta & -\sin\bigl(\theta-\frac{2\pi}{3}\bigr) & -\sin\bigl(\theta+\frac{2\pi}{3}\bigr)
\[1ex]
1/\sqrt{2} & 1/\sqrt{2} & 1/\sqrt{2}
\end{bmatrix}
]
\end{document}

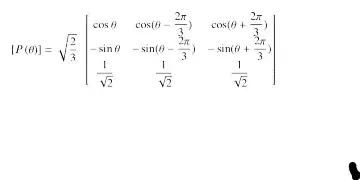
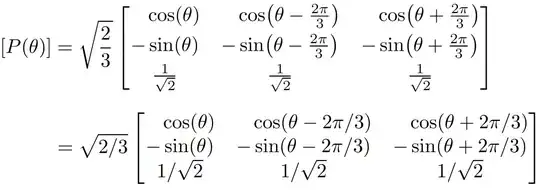




amsmathenvironmentvmatrixwould therefore be suitable. – barbara beeton Apr 29 '23 at 13:39