4

I have the following minimal working example:

\documentclass{standalone}

\usepackage{tikz}
\usetikzlibrary{calc}


\begin{document}
\begin{tikzpicture}
\coordinate (A) at (-1, 1);
\coordinate (B) at (2, 2);


\draw (A) -- (B);
\draw[dashed] let \p1 = (A), \p2 = (B) in (B) -- (5, {((\y2-\y1)/(\x2-\x1))*(5-\x1) + \y1});
\end{tikzpicture}
\end{document}

One knows that the line equation can be calculated with

y-y0 = m(x-x0)

where the slope m = (y1-y0)/(x1-x0).

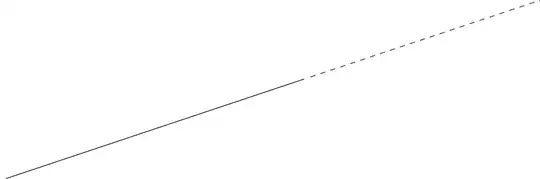
Here, you can see that x = 5 in my case but the new line doesn't follow the original line as expected. Instead I get the following:

enter image description here

However when choosing x = 0 it works somehow. I'm lost on why it isn't working like expected for the other points.

Fabitastic
  • 43

2 Answers2

6

Once a coordinate is evaluated PGF/TikZ only knows its position in the canvas coordinate system (with units). The xyz coordinate system just transform your x, y and z values (without units) into the canvas coordinate system. (By default, for x and y this means just multiplication with 1cm.)

The \x and \y shorthands only return values in the canvas coordinate system and indeed letting TeX write

((\y2-\y1)/(\x2-\x1))*(5-\x1) + \y1

on the page or the log file will result in

((56.90549pt-28.45274pt)/(56.90549pt–28.45274pt))*(5–28.45274pt) + 28.45274pt

The lonely 5 will now be interpreted as 5pt and not 5 (or 5cm).

One solution would be to parse (5, <any y value>) in \p3 and use \x3 instead of 5 or you can use the undocumented intersection of coordinate specification and just let TikZ to the math for you, i.e. find the point where the line through A and B meets the vertical line through x = 5.

Code

\documentclass[tikz]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\coordinate (A) at (-1, 1);
\coordinate (B) at (2, 2);

\draw (A) -- (B);
\draw[dashed] let \p1 = (A),
                  \p2 = (B),
                  \p3 = (5,0) in
  (B) -- (5, {((\y2-\y1)/(\x2-\x1))*(\x3-\x1) + \y1});
\end{tikzpicture}
\begin{tikzpicture}
\coordinate (A) at (-1, 1);
\coordinate (B) at (2, 2);


\draw (A) -- (B);
\draw[dashed] (B) -- (intersection of A--B and 5,0--5,1);
\end{tikzpicture}
\end{document}

Output

enter image description here

Qrrbrbirlbel
  • 119,821
  • Of course, you can also use -1, 1, 2 and 2 inside PGFMath but then you will need to have your own macros/functions for those and make the coordinate specification dependent on those values, too. – Qrrbrbirlbel Jun 01 '23 at 15:02
1

Using tzplot:

enter image description here

\documentclass{standalone}

\usepackage{tzplot}


\begin{document}


\begin{tikzpicture}
\tzcoors(-1,1)(A)(2,2)(B);
\tzLFn(A)(B)[-1:5]<edge[dashed,blue] ([turn]0:5cm)> % to extend
\end{tikzpicture}


\end{document}

Similarly, you can also:

\documentclass{standalone}

\usepackage{tzplot}


\begin{document}


\begin{tikzpicture}
\tzcoors(-1,1)(A)(2,2)(B);
\tzLFn(A)(B)[-1:5]
\tzpointangle(A)(B){\angleAB} % calculate the angle
\tzLFndashed{tan(\angleAB)}[5:10]
\end{tikzpicture}


\end{document}
I. Cho
  • 2,985