3

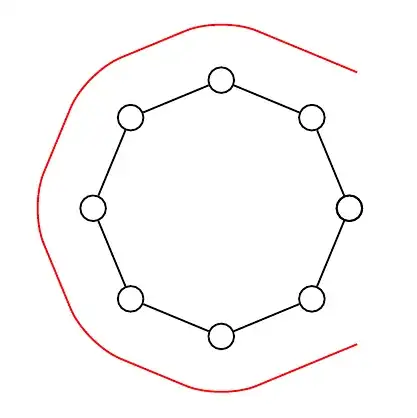
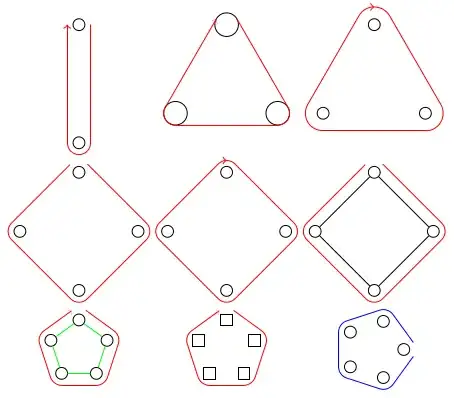
I would like to draw a figure indicating a path being traversed on a fixed graph, like the following (red) loop on the given (black) graph:

enter image description here

which I produced in this case using the following terrible code:

\documentclass{amsart}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
    [vertex/.style={circle, inner sep=0pt,minimum size=4mm}]    
    \node (A) [vertex] at (90:1) {};
    \node (B) [vertex] at (330:1) {};
    \node (C) [vertex] at (210:1) {};
    \draw (A) circle (1mm);
    \draw (B) circle (1mm);
    \draw (C) circle (1mm);
    \draw (A) -- (B) -- (C) -- (A);
    \draw[red,->] 
        (A.30) 
        -- (B.30) arc (30:-90:2mm)
        -- (C.270) arc (270:150:2mm)
        -- (A.150);
\end{tikzpicture}
\end{document}

I would like do this in a less terrible way so that (a) it doesn't break when I change basic parameters like the node size or location, and (b) I don't have to calculate weird angles when the node placement is different or when the graph is more complicated, etc.

In general paths can be long and complicated, and they may backtrack or reuse edges, for example ABCBA describes a path on the graph above (once you label the nodes). I would like to be able to draw things like this.

My true hope is to have code and/or macros that let me relatively easily generate the red path from a sequence of graph nodes. I am willing to tinker and customize individual paths and am not expecting the whole process to be automated. In the resulting image, the whole path should be visible.

Thanks in advance for any suggestions.

aaron
  • 131

3 Answers3

5

Let's try to answer this one point by point.

  1. is there a way to obtain a graph that is modular i.e. you can change many parameters and the graph doesn't break?

yes, here is the code:

    [vertex/.style={circle, inner sep=0pt,minimum size=4mm}]    
        \node (A) [vertex] at (90:1) {};
        \node (B) [vertex] at (330:1) {};
        \node (C) [vertex] at (210:1) {};

    \draw (A) circle (1mm);
    \draw (B) circle (1mm);
    \draw (C) circle (1mm);
    \draw (A) -- (B) -- (C) -- (A);

    \coordinate (a0) at ($(A) + (180:3mm) $);   
    \coordinate (d)  at ($(A) + (0:3mm) $);
    \coordinate (e)  at ($(B) + (-30:3mm) $);
    \coordinate (f)  at ($(C) + (-90-60:3mm) $);    

    \draw[rounded corners](d) -- (e) --(f) -- (a0);

The very first thing I did is use coordinateto define 4 points that are defined according to the already existing A,B,C nodes.

How? by using the calc tikzlibrary. The syntax is ($(A) + (180:3mm) $) i.e grab the position of A add to it this value. the value here being a position defined in the polar system (angle:radius). Like you already did.

Then, draw a path that goes through the 4 coordinates but with rounded corners.

Modularity accomplished.

Next step: generalisation, which is harder.

First question : can I make the distance between red and black parametric?

yes, I can add \def\radius{3} line inside the tikzpicture and replace the 3 of 3 mm.

enter image description here

Let's automate all of this


    \begin{tikzpicture}[vertex/.style={draw, circle, inner sep=0pt, minimum size=2mm}]    
        \def\nodescount{8}
        \def\radius{5}

    \foreach \X [remember=\X as \lastx (initially 0)] in {0,1,...,\nodescount}{
        \node (A\X) [vertex] at (\X*360/\nodescount:1) {};
        \draw (A\lastx)--(A\X);
        \coordinate (B\X) at ($(A\X) + (\X*360/\nodescount:\radius mm) $);  
    }
    \draw [red,rounded corners=3mm] (B1)-- (B2)--(B3) --(B4) --(B5)--(B6) --(B7);
\end{tikzpicture}

enter image description here

using a foreachloop that leverages \def\nodescount{8} to create 8 nodes by dividing 360° into 8 parts. Link each node with the previous one via [remember=\X as \lastx (initially 0)]. Define the needed coordinate for the red path.

I could not automate plotting the red part due to some inconsistency. I need to work on that.

Finally, bear in mind that there are better ways and tools to do this. This is a possible solution that is pure tikz. I enjoyed just making it.

anis
  • 1,510
  • 5
  • 13
  • Thank you . . . what "better ways and tools" do you have in mind? – aaron Jun 16 '23 at 22:18
  • this is called a Convex Hull. OpenCV, python, have the implementation of such algorithm. The term convex hull appears in the documentation of Tikz but there is no function or library to have it. – anis Jun 17 '23 at 06:55
  • You may also use toll like GIMP, Photoshop or Blender. I can imagine a way were I duplicate a layer, scale is from the centre a bit and then define a path. – anis Jun 17 '23 at 06:56
  • 1
    I thought about this solution with rounded corners, too, and had already typed up a comment, but somehow I was unnsatisfied with it (because the lines are farther away from the nodes on the start and end point of the hull), nonetheless good answer :) – Skillmon Jun 17 '23 at 17:54
2

The following works for an arbitrary number of nodes bigger 2. The nodes are regularly placed. You have a few options to tune this to your liking.

It doesn't use rounded corners as that gives imperfect placement of the start and end of the path around the nodes. Instead this uses arcs.

\documentclass[border=3.14,tikz]{standalone}

\usetikzlibrary{calc}


\makeatletter
\newif\ifpwp@closed
\newif\ifpwp@straights
\pgfqkeys{/pwp}
  {
    .is family
    ,radius/.initial = 1
    ,start angle/.initial = 90
    ,vertex/.style = {draw, circle}
    ,vertex/radius/.initial = 1mm
    ,path/.style = {->, red}
    ,path/radius/.initial = 2mm
    ,path/closed/.is if = pwp@closed
    ,prefix/.code = {\def\pwp@coord##1{#1-@Alph{##1}}}
    ,draw straights/.is if = pwp@straights
    ,straights/.style = {}
  }
\newcommand\pwp@coord[1]{@Alph{#1}}
\newcommand\pwp@val[1]{\pgfkeysvalueof{/pwp/#1}}
\newcommand\polygonwithpath[2][]
  {%
    \begingroup
      \pgfqkeys{/pwp}{#1}%
      \pgfmathsetmacro\pwp@angle{360/#2}%
      \foreach\i in {1,...,#2}
        {
          \node
            [/pwp/vertex,minimum size=2\pwp@val{vertex/radius},inner sep=0pt]
            (\pwp@coord{\i})
            at ({\pwp@val{start angle} - \pwp@angle  (\i-1)}:\pwp@val{radius})
            {}
            ;
        }
      \ifpwp@straights
        \draw[/pwp/straights] (\pwp@coord{#2}) -- (\pwp@coord{1})
          \foreach\i in{2,...,#2}{(\pwp@coord{\numexpr\i-1})--(\pwp@coord\i)}
          ;
      \fi
      \xdef\pwp@path
        {%
          \ifpwp@closed
            ($(\pwp@coord{1})+(\pwp@val{start angle}:\pwp@val{path/radius})$)
            arc[start angle=\pwp@val{start angle}, end angle=\pwp@val{start angle}-\pwp@angle/2]
          \else
            ($(\pwp@coord{1})+(\pwp@val{start angle}-\pwp@angle/2:\pwp@val{path/radius})$)
          \fi
        }%
      \foreach\i in {2,...,#2}
        {%
          \xdef\pwp@path
            {%
              \pwp@path
              --
              ($(\pwp@coord{\i})+({\pwp@val{start angle}-(\i-1.5)\pwp@angle}:\pwp@val{path/radius})$)
              arc[start angle=\pwp@val{start angle}-(\i-1.5)\pwp@angle, end
              angle=\pwp@val{start angle}-(\i-0.5)\pwp@angle]
            }%
        }%
      \xdef\pwp@path
        {%
          \noexpand\draw
            [%
              /pwp/path,
              radius = \pwp@val{path/radius},
            ]%
          \pwp@path
          --($(\pwp@coord{1})+({\pwp@val{start angle}-(#2-0.5)\pwp@angle}:\pwp@val{path/radius})$)
          \ifpwp@closed
          arc[start angle=\pwp@val{start angle}-(#2-0.5)*\pwp@angle, end angle=-270]
          \fi
          ;%
        }%
      \pwp@path
    \endgroup
  }
\makeatother


\begin{document}
\begin{tikzpicture}
  \polygonwithpath{2}
  \begin{scope}[xshift=25mm]
    \polygonwithpath[vertex/radius=2mm]{3}
    \begin{scope}[xshift=25mm]
      \polygonwithpath[path/radius=3mm,path/closed]{3}
    \end{scope}
  \end{scope}
  \begin{scope}[yshift=-25mm]
    \polygonwithpath{4}
    \begin{scope}[xshift=25mm]
      \polygonwithpath[path/closed = true]{4}
      \begin{scope}[xshift=25mm]
        \polygonwithpath[draw straights]{4}
      \end{scope}
    \end{scope}
    \begin{scope}[yshift=-20mm]
      \polygonwithpath[radius=5mm, draw straights, straights/.style=green]{5}
      \begin{scope}[xshift=25mm]
        \polygonwithpath[radius=5mm,vertex/.style={draw}]{5}
        \begin{scope}[xshift=25mm]
          \polygonwithpath[radius=5mm,path/.style={blue},start angle=0]{5}
        \end{scope}
      \end{scope}
    \end{scope}
  \end{scope}
\end{tikzpicture}
\end{document}

enter image description here

Skillmon
  • 60,462
2

Using the nfold library helps with creating a parallel line. Combining this with the spath3 library can help us slice two of those together.

Unfortunately, using the rounded corners options creates troubles with both of them at different points but there's something to start with.

For a simple convex hull, only nfold is necessary and using it with a round line join creates good results.

Code

\documentclass[tikz]{standalone}
\usetikzlibrary{arrows.meta, graphs.standard, nfold}
\usetikzlibrary{spath3}
\makeatletter
\tikzset{
  offset round/.code=
    \tikz@addmode{%
      \pgfsetroundjoin         \pgfgetpath   \tikz@temp
      \pgfsetpath\pgfutil@empty\pgfoffsetpath\tikz@temp{#1}}}
\makeatother
\tikzset{
  vertex/.style={circle, inner sep=+0pt, minimum size=+2mm, draw},
  graphs/every graph/.append style={nodes=vertex, clockwise, typeset=}}
\begin{document}
\begin{tikzpicture}
\graph[n=3]{subgraph C_n};
\draw[red, ->] plot[samples at={1, 2, 3, 1}] (\x) [offset round=2mm];
\end{tikzpicture}

\begin{tikzpicture}
\graph[n=3]{subgraph C_n};
\path plot[samples at={1, 2, 3, 1}] (\x) [offset round=+ 2mm, spath/save=p];
\path plot[samples at={1, 3, 2, 1}] (\x) [offset round=+-4mm, spath/save=q];
\draw[->, red, spath/use=p] -- (spath cs:q 0) [spath/use={q, weld}];
\end{tikzpicture}


\begin{tikzpicture}
\graph[n=6]{subgraph I_n, 1 -- 2 -- 3 -- 1 -- 6 -- 4};
\draw[red, ->] plot[samples at={1, 2, 3, 1, 6, 4}] (\x) [offset round=2mm];
\end{tikzpicture}
\end{document}

Output

enter image description here enter image description here enter image description here

Qrrbrbirlbel
  • 119,821