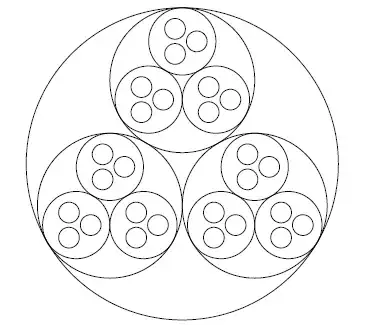
I want to draw the following figure:
The accepted answer of SebGlav from this post gives some code.
The code (due to SebGlav):
\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{calc}
\begin{document}
\newcommand{\RadiusA}{8} %Define the radius of big-boundary circle
\pgfmathsetmacro{\RadiusB}{\RadiusA/(1+2/sqrt(3))}
\begin{tikzpicture}
\draw[] (0,0) circle[radius=\RadiusA cm];
\foreach \ang [count = \i from 1] in {90,210,330}
\draw[] (\ang:\RadiusA-\RadiusB) coordinate (center-\i) circle[radius=\RadiusB cm];
\pgfmathsetmacro{\RadiusC}{\RadiusB/(1+2/sqrt(3))}
\foreach \i in {1,2,3}
\foreach \ang in {90,210,330}
\draw[] ($(center-\i)+(\ang:\RadiusB-\RadiusC)$) circle[radius=\RadiusC cm];
% Divide each small circle into 3 equal circles
\foreach \i in {1,2,3}
\foreach \ang in {90,210,330}
\foreach \j in {0,1,2}
\draw[] ($(center-\i)+(\ang:\RadiusB-\RadiusC)+(120*\j:\RadiusB/3)$) circle[radius=\RadiusB/6];
%this is the main governng equation for small circles
\end{tikzpicture}
\end{document}
plotted the following figure:
But the above figure can further be improved by improving the last governing equation
\draw[] ($(center-\i)+(\ang:\RadiusB-\RadiusC)+(120*\j:\RadiusB/5)$) circle[radius=\RadiusB/7];
as follows:
The later figure is much better, but still not what I require. We need to make sure the three small circles touch each other, as in the image in my question above.
I think we have to adjust the main governing equation at the end of the code. I appreciate suggestions.



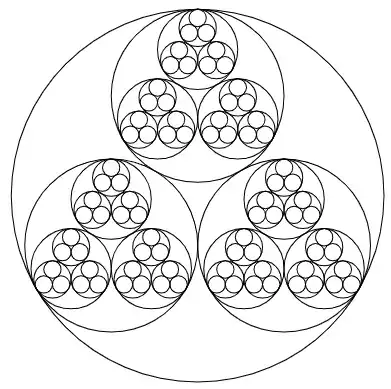
\draw[] ($(center-\i)+(\ang:\RadiusB-\RadiusC)+(120*\j:\RadiusB/5)$) circle[radius=\RadiusB/7];needs to be improved. I am unable to do it. – learner Sep 08 '23 at 05:13\draw[] ($(center-\i)+(\ang:\RadiusB-\RadiusC)+(120*\j:\RadiusB/5)$) circle[radius=\RadiusB/7];but it is not giving as expected. Maybe I am making something wrong in the division of the circle – learner Sep 08 '23 at 05:15