Tikz rotation sequence

Question

I am quite new to Latex. I want to create a figure representing the slip systems of unit cells in different crystal orientations. I am using TikZ and was able able to create the figures for the 100 and 110 orientations. However, I am struggling to create the figure for the 111 crystal orientation, since a rotation around two axes is necessary, namely 45 degrees around z and 54.74 degrees around the x axis. The first rotation works fine, but the second rotation is using the already rotated x axis instead of the original x axis. Is there any trick on how to achieve this?

This is my code as an example of one of the four slip systems with a 100 crystal orientation that is to be rotated (no rotation applied here):

\documentclass{article}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{arrows.meta,3d}
\begin{document}
\begin{figure}[h!]
    \centering
\tdplotsetmaincoords{60}{60} 
\begin{tikzpicture}[scale=1,tdplot_main_coords]
\draw[-latex, blue] (0,0,0) -- (5,0,0) node[anchor=north east]{$x$};
\draw[-latex, blue] (0,0,0) -- (0,5,0) node[anchor=north west]{$y$};
\draw[-latex, blue] (0,0,0) -- (0,0,5) node[anchor=south]{$z$};
\def\size{2}
\begin{scope}     
        \coordinate (A0) at (0,0,0);
        \coordinate (A1) at (0,0,\size);
        \coordinate (A2) at (0,\size,0);
        \coordinate (A3) at (0,\size,\size);
        \coordinate (A4) at (\size,0,0);
        \coordinate (A5) at (\size,0,\size);
        \coordinate (A6) at (\size,\size,0);
        \coordinate (A7) at (\size,\size,\size);
        \draw[black,dashed] (A0) -- (A1);
        \draw[black,dashed] (A0) -- (A2);
        \draw[black,dashed] (A0) -- (A4);
        \fill[red, opacity=0.3] (A0) -- (A3) -- (A6) -- cycle;
        \draw[-{Stealth[length=4mm]}, thick, red] (A0) -- (A3);
        \draw[-{Stealth[length=4mm]}, thick, red] (A0) -- (A6);
        \draw[-{Stealth[length=4mm]}, thick, red] (A6) -- (A3);
    \draw[black] (A2) -- (A3);
    \draw[black] (A2) -- (A6);
    \draw[black] (A3) -- (A1);
    \draw[black] (A3) -- (A7);
    \draw[black] (A4) -- (A6);
    \draw[black] (A4) -- (A5);
    \draw[black] (A5) -- (A1);
    \draw[black] (A5) -- (A7);
    \draw[black] (A6) -- (A7);
\end{scope}

\end{tikzpicture}
\caption{Slip systems for a $\langle 100\rangle$ orientation.}
    \label{fig:enter-label}
\end{figure}
\end{document}

Producing this figure:

And here is my attempt to represent the 111 crystal orientation:

\documentclass{article}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{arrows.meta,3d}
\begin{document}
\begin{figure}[h!]
    \centering
\tdplotsetmaincoords{60}{60} 
\begin{tikzpicture}[scale=1,tdplot_main_coords]
\draw[-latex, blue] (0,0,0) -- (5,0,0) node[anchor=north east]{$x$};
\draw[-latex, blue] (0,0,0) -- (0,5,0) node[anchor=north west]{$y$};
\draw[-latex, blue] (0,0,0) -- (0,0,5) node[anchor=south]{$z$};
\def\size{2}
\begin{scope}[rotate around z = 45, rotate around y = 54.74]     
        \coordinate (A0) at (0,0,0);
        \coordinate (A1) at (0,0,\size);
        \coordinate (A2) at (0,\size,0);
        \coordinate (A3) at (0,\size,\size);
        \coordinate (A4) at (\size,0,0);
        \coordinate (A5) at (\size,0,\size);
        \coordinate (A6) at (\size,\size,0);
        \coordinate (A7) at (\size,\size,\size);
        \draw[black,dashed] (A0) -- (A1);
        \draw[black,dashed] (A0) -- (A2);
        \draw[black,dashed] (A0) -- (A4);
        \fill[red, opacity=0.3] (A0) -- (A3) -- (A6) -- cycle;
        \draw[-{Stealth[length=4mm]}, thick, red] (A0) -- (A3);
        \draw[-{Stealth[length=4mm]}, thick, red] (A0) -- (A6);
        \draw[-{Stealth[length=4mm]}, thick, red] (A6) -- (A3);
    \draw[black] (A2) -- (A3);
    \draw[black] (A2) -- (A6);
    \draw[black] (A3) -- (A1);
    \draw[black] (A3) -- (A7);
    \draw[black] (A4) -- (A6);
    \draw[black] (A4) -- (A5);
    \draw[black] (A5) -- (A1);
    \draw[black] (A5) -- (A7);
    \draw[black] (A6) -- (A7);
\end{scope}

\end{tikzpicture}
\caption{Slip systems for a $\langle 100\rangle$ orientation.}
    \label{fig:enter-label}
\end{figure}
\end{document}

Producing this figure:

Is there any way to make this work in TikZ? Also I am using Overleaf for writing, if this is of any interest.

I appreciate any help on making this work since I have spent quite some time on this and am not able to make it work...

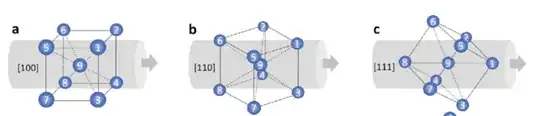
Edit: This image is similar to what I am trying to achieve, but with the reference sample surface being at the left (or right), so the z-axis of my images would be horizontally here. So for the <111> Orientation the {111} plane (red triangle in my images) is parallel to the sample surface (or parallel to the x-y-plane in regards of a x-y-z-system)

@Mensch thank you:) Any ideas on how I can achieve the desired outcome? — mattka, Nov 05 '23 at 17:19
Can you please show us what you are trying to draw? I have no idea what a 111 crystal orientation should look like:) The web page https://www.universitywafer.com/silicon-wafer-orientation.html has similar pictures, all of which are easy to draw in TikZ. If the pictures on this web page suffice, then I can show you how to draw them. — 314159265358979323, Nov 06 '23 at 06:21
Tank you @314159265358979323!:) The pictures on the pages you linked is showing the crystallographic planes {100}, {110} and {111}. In my pictures the red triangular plane is one of four possible 111 planes. To achieve a crystal orientation of <111> I want to rotate the cube in a way so that the {111} plane is on the x-y-plane (plane normal parallel to z). I have edited my post and added an image which is similar to what I am trying to achieve. Note the rotated representation (their z-axis is horizontal, from left to right) — mattka, Nov 06 '23 at 11:00
Perhaps this post helps: https://tex.stackexchange.com/questions/67573/tikz-shift-and-rotate-in-3d ? — 314159265358979323, Nov 06 '23 at 11:53
@314159265358979323 There's a deleted 'answer' there which is really a question and I think the same as the OP's here: how to do two rotations. And the problem mentioned is the same. — cfr, Nov 06 '23 at 15:32
@314159265358979323 Thank you for the hint, I will try it later today. I will post it here, if I find a solution based on this! — mattka, Nov 06 '23 at 15:48

score 2 · Answer 1 · answered Nov 09 '23 at 06:31

My first impression, if I understand correctly what you would like to obtain, is that there is a problem of order in the rotations. The way you wrote your code, you do a rotation around x and then around z. (By the way, there is a mistake any you wrote y instead of x.) In the question (your text), you are talking about z first and x after.

You can see both results in the figure.

Some remarks

The dashed edges are misleading since the cube is changing with respect to the point of view.
I use a different point of view to better grasp the outcome of the composed rotations.
The way you named the vertices is strange!
My code below is long since there are three drawings. But it is almost your code for the cube set into a pic element.

The code

\documentclass{article}
\usepackage[top=100pt, bottom=75pt, left=75pt, right=75pt]{geometry}
\setlength{\headsep}{15pt}
\setlength{\footskip}{45pt}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{arrows.meta,3d}
\usetikzlibrary{math}
\begin{document}
\tikzset{%
  vertex/.style={scale=.6, fill=orange, fill opacity=.2,
    text=blue, text opacity=1},
  pics/crystal x and z/.style 2 args={%
    code={%
      \begin{scope}[rotate around z=#2, rotate around x=#1]

        \path (0,0,0) coordinate (A0) node[vertex] {$0$};
        \path (0,0,\size) coordinate (A1) node[vertex] {$1$};
        \path (0,\size,0) coordinate (A2) node[vertex] {$2$};
        \path (0,\size,\size) coordinate (A3) node[vertex] {$3$};
        \path (\size,0,0) coordinate (A4) node[vertex] {$4$};
        \path (\size,0,\size) coordinate (A5) node[vertex] {$5$};
        \path (\size,\size,0) coordinate (A6) node[vertex] {$6$};
        \path (\size,\size,\size) coordinate (A7) node[vertex] {$7$};
        \fill[red, opacity=0.3] (A0) -- (A3) -- (A6) -- cycle;
        \draw[-{Stealth[length=1ex]}, red] (A0) -- (A3);
        \draw[-{Stealth[length=1ex]}, red] (A0) -- (A6);
        \draw[-{Stealth[length=1ex]}, thick, green!50!black] (A6) -- (A3);
    \draw[black] (A0) -- (A1);
    \draw[black] (A0) -- (A2);
    \draw[black] (A0) -- (A4);
    \draw[black] (A2) -- (A3);
    \draw[black] (A2) -- (A6);
    \draw[black] (A3) -- (A1);
    \draw[black] (A3) -- (A7);
    \draw[black] (A4) -- (A6);
    \draw[black] (A4) -- (A5);
    \draw[black] (A5) -- (A1);
    \draw[black] (A5) -- (A7);
    \draw[black] (A6) -- (A7);
  \end{scope}
}

},
  pics/crystal z and x/.style 2 args={%
    code={%
      \begin{scope}[rotate around x=#2, rotate around z=#1]

        \path (0,0,0) coordinate (A0) node[vertex] {$0$};
        \path (0,0,\size) coordinate (A1) node[vertex] {$1$};
        \path (0,\size,0) coordinate (A2) node[vertex] {$2$};
        \path (0,\size,\size) coordinate (A3) node[vertex] {$3$};
        \path (\size,0,0) coordinate (A4) node[vertex] {$4$};
        \path (\size,0,\size) coordinate (A5) node[vertex] {$5$};
        \path (\size,\size,0) coordinate (A6) node[vertex] {$6$};
        \path (\size,\size,\size) coordinate (A7) node[vertex] {$7$};
        \fill[red, opacity=0.3] (A0) -- (A3) -- (A6) -- cycle;
        \draw[-{Stealth[length=1ex]}, red] (A0) -- (A3);
        \draw[-{Stealth[length=1ex]}, red] (A0) -- (A6);
        \draw[-{Stealth[length=1ex]}, thick, green!50!black] (A6) -- (A3);
    \draw[black] (A0) -- (A1);
    \draw[black] (A0) -- (A2);
    \draw[black] (A0) -- (A4);
    \draw[black] (A2) -- (A3);
    \draw[black] (A2) -- (A6);
    \draw[black] (A3) -- (A1);
    \draw[black] (A3) -- (A7);
    \draw[black] (A4) -- (A6);
    \draw[black] (A4) -- (A5);
    \draw[black] (A5) -- (A1);
    \draw[black] (A5) -- (A7);
    \draw[black] (A6) -- (A7);
  \end{scope}
}

}
}
\begin{figure}[h!]
  \centering
  \tdplotsetmaincoords{75}{165} 
  \begin{tikzpicture}[scale=.7, tdplot_main_coords,
    evaluate={\size = 2; \a = 3.5;}]
    \draw[-latex, blue] (0,0,0) -- (\a,0,0) node[anchor=north east]{$x$};
    \draw[-latex, blue] (0,0,0) -- (0,\a,0) node[anchor=north west]{$y$};
    \draw[-latex, blue] (0,0,0) -- (0,0,\a) node[anchor=south]{$z$};
    \path (0, 0) pic {crystal x and z={0}{0}};

  \end{tikzpicture}
  \qquad
  \begin{tikzpicture}[scale=.7, tdplot_main_coords,
    evaluate={\size = 2; \a = 3.5;}]
    \draw[-latex, blue] (0,0,0) -- (\a,0,0) node[anchor=north east]{$x$};
    \draw[-latex, blue] (0,0,0) -- (0,\a,0) node[anchor=north west]{$y$};
    \draw[-latex, blue] (0,0,0) -- (0,0,\a) node[anchor=south]{$z$};
    \path (0, 0) pic {crystal x and z={54.74}{0}};

  \end{tikzpicture}
  \qquad
  \begin{tikzpicture}[scale=.7, tdplot_main_coords,
    evaluate={\size = 2; \a = 3.5;}]
    \draw[-latex, blue] (0,0,0) -- (\a,0,0) node[anchor=north east]{$x$};
    \draw[-latex, blue] (0,0,0) -- (0,\a,0) node[anchor=north west]{$y$};
    \draw[-latex, blue] (0,0,0) -- (0,0,\a) node[anchor=south]{$z$};
    \path (0, 0) pic {crystal x and z={54.74}{45}};
  \end{tikzpicture}
  \caption{Rotations around $Ox$ first and $Oz$ second}
  \label{fig:enter-label}
\end{figure}
\begin{figure}[h!]
  \centering
  \tdplotsetmaincoords{75}{165} 
  \begin{tikzpicture}[scale=.7, tdplot_main_coords,
    evaluate={\size = 2; \a = 3.5;}]
    \draw[-latex, blue] (0,0,0) -- (\a,0,0) node[anchor=north east]{$x$};
    \draw[-latex, blue] (0,0,0) -- (0,\a,0) node[anchor=north west]{$y$};
    \draw[-latex, blue] (0,0,0) -- (0,0,\a) node[anchor=south]{$z$};
    \path (0, 0) pic {crystal z and x={0}{0}};

  \end{tikzpicture}
  \qquad
  \begin{tikzpicture}[scale=.7, tdplot_main_coords,
    evaluate={\size = 2; \a = 3.5;}]
    \draw[-latex, blue] (0,0,0) -- (\a,0,0) node[anchor=north east]{$x$};
    \draw[-latex, blue] (0,0,0) -- (0,\a,0) node[anchor=north west]{$y$};
    \draw[-latex, blue] (0,0,0) -- (0,0,\a) node[anchor=south]{$z$};
    \path (0, 0) pic {crystal z and x={45}{0}};

  \end{tikzpicture}
  \qquad
  \begin{tikzpicture}[scale=.7, tdplot_main_coords,
    evaluate={\size = 2; \a = 3.5;}]
    \draw[-latex, blue] (0,0,0) -- (\a,0,0) node[anchor=north east]{$x$};
    \draw[-latex, blue] (0,0,0) -- (0,\a,0) node[anchor=north west]{$y$};
    \draw[-latex, blue] (0,0,0) -- (0,0,\a) node[anchor=south]{$z$};
    \path (0, 0) pic {crystal z and x={45}{54.74}};
  \end{tikzpicture}
  \caption{Rotations around $Oz$ first and $Ox$ second}
  \label{fig:enter-label}
\end{figure}
\end{document}

Tikz rotation sequence

1 Answers1