How to fix the syntax of \draw (i-2) circle let \p{dgcr} = (i-2) in node at (i-2) {$d_{g,cr} = \fpeval{\x{dgcr}/0.35}$}; to make the node calculated number correct (i.e., it should be around 0.6, not 316)?
\documentclass{article}
\usepackage{pgfplots}
\usetikzlibrary{calc, intersections}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
xmin = 0, xmax = 0.4,
ymin = 0, ymax = 0.6,
xtick distance = {0.2},
ytick distance = {0.2},
minor tick num = 1,
grid = both,
]
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\addplot
[
domain = 0:1.5,
samples = 100,
black,
variable = dg,
name path = OptBrakingDist,
] (
{ dg / 2.5 * (1.2 - dg * 0.5) },
{ dg / 2.5 * (1.3 + dg * 0.5) }
);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\addplot
[
domain = 0:\fpeval{1/(1 - 0.35)},
%samples = 2,
blue,
variable = dg,
name path = fixeddist,
]
( { 0.35 * dg } , { (1 - 0.35) * dg } )
;
%%%%%%%%%%%%%%%%%%%%%%%%
% Find and label the intersections
\path [name intersections = {of = fixeddist and OptBrakingDist, name=i}];
%
\draw[fill=red, draw=none] (i-2) circle [radius=3pt] let \p{dgcr} = (i-2) in node[left=3pt, inner sep=0pt, fill=white, scale=0.75] at (i-2) {$d_{g,cr} = \fpeval{\x{dgcr}/0.35}$};
\end{axis}
\end{tikzpicture}
\end{document}

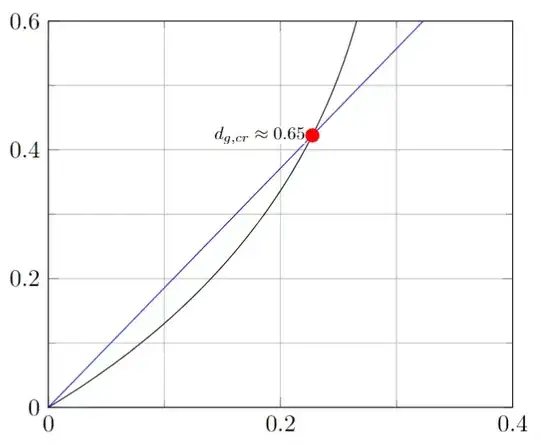
\pgfextractxand\pgfextractyuse length registers and usually\pgfpointanchor, while\pgfgetlastxyuses macros, typically after\pathlocates the point. – John Kormylo Dec 05 '23 at 22:07\newdimen\mydim \pgfextractx\mydim{\pgfpointanchor{i-2}{center}} \draw (i-2) circle node at (i-2) {$d_{g,cr} = \fpeval{\mydim/0.35}$};throws the errorNo shape named i-2 is known. – Diaa Dec 06 '23 at 06:32\extractcoord\x\y{i-2} \draw (i-2) circle node at (i-2) {$d_{g,cr} = \fpeval{round(\x/0.35, 1)}$};prints650, not0.7as expected. – Diaa Dec 06 '23 at 06:36\pgfplotsextra. Actually, you can move the entire intersections calculations outside the axis environment, since the path names are stored globally. OTOH, they give tikz coordinates in pt, not whatever units pgfplots uses for axis cs: coordinates. – John Kormylo Dec 06 '23 at 16:42