I have the following equations:
Now I want to shift the $2^{2k}$ and $2^k$ in the last three lines to the right, just before the $\geq$ sign. How can I achieve that without hardcoding?
Here is my MWE:
\documentclass[ngerman, fontsize=11pt, DIV=12 ,BCOR = 10mm, parskip=half-, twoside]{scrbook}
\usepackage{amsmath}
\begin{document}
\begin{alignat}{2}
&2^k\cdot (2^k-h)&&\geq 1 \
\Longleftrightarrow
&2^{2k}-h\cdot 2^k&&\geq 1 \
\Longleftrightarrow
&2^{2k}&&\geq h\cdot 2^k+1 \
\Longleftrightarrow
&2^k &&\geq \sqrt{h\cdot 2^k+1} \
\Longleftrightarrow
&2^k &&\geq \sqrt{n}.
\end{alignat}
\end{document}
When I change 2^{2k}& to &2^{2k} I get additional space in the frst two lines.


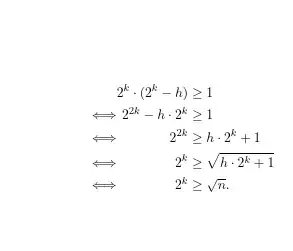


2^{2k}&to&2^{2k}, also you want\Longleftrightarrow{}to get the correct spacing back if you have the arrow to the left of the&– David Carlisle Jan 15 '24 at 17:44