As far as the author of the initial release of this answer knows, TeX by means of registers and primitives can do arithmetic in the range -231+1 to +231-1.
If
- you need this only for integers and fractions ½ and
- you don't mind reducing to a range of -230+1 to +230-1,
then you can have TeX maintain
- a macro
\doublesum, which, instead of wasting a \count-register, is to hold the double of the sum to calculate,
- a macro
\thesum, which delivers the result of halving \doublesum as a sequence of digits and probably one instance of \frac{1}{2},
- a macro
\addtosum, which is used for adding the double of its argument to \doublesum,
- a macro
\clearsum, which defines \doublesum empty.
(By the way, \sum is already defined in TeX/LaTeX and is used for obtaining in mathematical typesetting the uppercase sigma with subscript/superscript limits for indices that is often used with sums of elements that are indexed. So don't be tempted to accidentally override \sum in the course of implementing your own "infrastructure" of macros that have the phrase "sum" in their name.)
The author of the initial release of this answer didn't bother implementing checking whether the argument of \addtosum is of correct form.
On the one hand implementing some sort of checking for restricting input to specific constellations of explicit character tokens out of specific classes of character tokens (signs, digits, spaces) trailed by at most one control word token \half is already shown in other answers.
On the other hand the question does not precisely specify what to consider "correct form".
E.g., if any TeX ⟨number⟩ quantity—⟨number⟩ is explained in Backus-Naur-notation in "Chapter 24: Summary of Vertical Mode" of the TeXbook; ε-TeX and pdfTeX and LuaTeX and XeTeX and other TeX engines extend the concept of TeX's ⟨number⟩—plus probably a single instance of the control word token \half surrounded by optional spaces is to be accepted, the question arises of how to interpret things like \numexpr\mycounter\relax\half while the current value of \mycounter is 0. Is that 0½? If so: As 0=-0, is 0½=-0½? Is that ½ or is that -½?
Besides this, expansion usually is not suppressed when TeX gathers tokens of a ⟨number⟩. Therefore proper checking would probably require implementing an algorithm in TeX for checking whether the tokens forming the argument expand to a set of tokens that forms valid ⟨optional signs⟩ or a complete valid ⟨number⟩ probably trailed by an optional control word token \half that might be surrounded by ⟨optional spaces⟩/⟨one optional space⟩ in case you manage to get that behind a control word token. So one would face the task of implementing an algorithm in TeX for checking the result of expansion. When it is about expansion of the tokens of an argument of a macro, these tokens themselves can be considered aspects of implementations of expansion-driven algorithms. So the task of implementing an algorithm for checking the result of expansion beneath other things would require checking whether the algorithm made up by the tokens that form the argument
- terminates without errors.
- terminates without unwanted side-effects that probably won't yield error messages (as in edge cases can happen, e.g., when arranging tokens of a macro argument so that expanding them leads to gobbling/re-arranging subsequent tokens that do not belong to the argument but are components of the ⟨replacement text⟩ of some macro's ⟨definition⟩—that macro in turn might belong to the macro-mechanism that forms the checking-routine…— and thus by the implementer of the macro-mechanism are intended as means for keeping the expansion-chain going properly).
- terminates at all.
This is not trivial in TeX and the author of the initial release of this answer is reminded of the halting problem.
\makeatletter
%-----------------------------------------------------------------------
\@ifdefinable\stopromannumeral{\chardef\stopromannumeral=`\^^00 }%
\newcommand\@twooftwo[2]{#1#2}%
%-----------------------------------------------------------------------
\newcommand\doublesum{}%
%-----------------------------------------------------------------------
\newcommand*\addtosum[1]{%
\edef\doublesum{%
\the\numexpr(0\doublesum)+(\addtosumSplitAtHalf#1\half Z\relax)%
\relax
}%
}%
\@ifdefinable\addtosumSplitAtHalf{%
\def\addtosumSplitAtHalf#1\half#2\relax{%
(#1+0)*2
\ifx#2Z\else
% The token \half is there, thus
% - in case the number is negative or 0 is prefixed by a
% minus sign subtract 1,
% - in case the number is positive or 0 is not prefixed by a
% minus sign add 1.
\ifnum\numexpr(#1+0)\relax=0 %
\ifnum\numexpr(#11)\relax<0 -\else+\fi
\else
\ifnum\numexpr(#1+0)\relax<0 -\else+\fi
\fi
1\fi
}%
}%
%-----------------------------------------------------------------------
\newcommand\clearsum{\def\doublesum{}}%
%-----------------------------------------------------------------------
\newcommand\thesum{%
\romannumeral
% Check if the integer-part of the sum is 0.
\ifnum
\numexpr
(0\doublesum)/2%
\ifodd\numexpr(0\doublesum)\relax
\ifnum\numexpr(0\doublesum)\relax>0 -\else+\fi1%
\fi
\relax=0 %
\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
% In case the integer-part of the sum is 0 and the doubled sum is
% even, no rounding occured, thus just print 0. In case of the
% doubled sum being odd, rounding occurred, so 1/2 or -1/2 needs
% to be delivered depending on whether the doubled sum is positive
% or negative.
\ifodd\numexpr(0\doublesum)\relax
\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\ifnum\numexpr(0\doublesum)\relax<0 %
\expandafter\stopromannumeral\expandafter-%
\else
\expandafter\stopromannumeral
\fi
\frac{1}{2}%
}%
{\stopromannumeral0}%
}{%
% In case the integer-part of the sum is not 0, calculate it
% by halving the doubled via \numexpr's division where rounding
% occurs in case the doubled sum is odd. In case of roundig
% and the number being positive subtract 1 otherwise add 1.
% In case of rounding also deliver 1/2.
\expandafter\stopromannumeral
\the\numexpr
(0\doublesum)/2%
\ifodd\numexpr(0\doublesum)\relax\ifnum\numexpr(0\doublesum)\relax
>0 -\else+\fi1\expandafter\@twooftwo\else\expandafter\@firstoftwo\fi
\relax{\frac{1}{2}}%
}%
}%
%-----------------------------------------------------------------------
% \addtosum and \clearsum can be prefixed by \global.
% Due to \romannumeral-expansion the result of \thesum is generated
% within two expansion steps.
%-----------------------------------------------------------------------
\makeatother
\documentclass{article}
\begin{document}
\global\clearsum (\thesum)
\par(\thesum - 7 = \global\addtosum{-7} \thesum)
\par(\thesum + 3 = \global\addtosum{3} \thesum)
\par(\thesum + 1\frac{1}{2} = \global\addtosum{1\half} \thesum)
\par(\thesum - 2\frac{1}{2} = \global\addtosum{-2\half} \thesum)
\par(\thesum + 5 = \global\addtosum{5} \thesum)
\par(\thesum + 7 = \global\addtosum{7} \thesum)
\par(\thesum - 3 = \global\addtosum{-3} \thesum)
\par(\thesum - 1\frac{1}{2} = \global\addtosum{-1\half} \thesum)
\par(\thesum + 2\frac{1}{2} = \global\addtosum{+2\half} \thesum)
\par(\thesum - 5 = \global\addtosum{-5} \thesum)
\par(\thesum - 1 = \global\addtosum{-1} \thesum)
\par(\thesum + \frac{1}{2} = \global\addtosum{0\half} \thesum)
\par(\thesum + \frac{1}{2} = \global\addtosum{\half} \thesum)
\par(\thesum + \frac{1}{2} = \global\addtosum{+\half} \thesum)
\par(\thesum + \frac{1}{2} = \global\addtosum{+0\half} \thesum)
\par(\thesum - \frac{1}{2} = \global\addtosum{-0\half} \thesum)
\par(\thesum - \frac{1}{2} = \global\addtosum{-\half} \thesum)
\par(\thesum - 0 = \global\addtosum{-0} \thesum)
\par(\thesum + 0 = \global\addtosum{+0} \thesum)
\par(\thesum + 0 = \global\addtosum{0} \thesum)
\par(\thesum + 0 = \global\addtosum{} \thesum)
\par(\thesum + 0 = \global\addtosum{+} \thesum)
\par(\thesum + 0 = \global\addtosum{-} \thesum)
\par(\thesum + 15\frac{1}{2} = \global\addtosum{15\half} \thesum)
\edef\SomeSumMacro{%
\unexpanded\expandafter\expandafter\expandafter{\thesum}%
}
\par The sum calculated so far is stored in the macro
\verb|\SomeSumMacro| whose meaning is:\
\texttt{\meaning\SomeSumMacro}
\end{document}

\documentclass{article}
\newcounter{sum}
\makeatletter
\def\mycommand#1{%
\afterassignment\get@args\count@=0#1\hfuzz#1\hfuzz}
\def\get@args#1\hfuzz#2\hfuzz{%
\if\relax\detokenize{#1}\relax
#2 is a number%
\addtocounter{sum}{#2}
\else
#2 is not a number%
\fi
}
[...]
\makeatother
[...]
I freely admit that part of my trouble is that I have only a superficial understanding of what's going on in the definition of \mycommand and \get@args to capture numbers,
[...]
\mycommand is a macro. When expanding it, TeX grabs an undelimited argument and delivers \mycommand's ⟨replacement text⟩ with the parameter #1 replaced by the tokens that form the argument. Expanding \mycommand yields the following:
\afterassignment\get@args
\count@=0⟨\mycommand's argument⟩\hfuzz⟨\mycommand's argument⟩\hfuzz
The \afterassignment-directive causes TeX to insert the token \get@args as soon as all tokens needed for doing the assignment to the \count-register denoted by the ⟨countdef token⟩ \count@ are gathered from the token-stream and processed:
As there is a leading 0, the process of gathering tokens belonging to the ⟨number⟩ of the assignment and hereby expanding things stops as soon as a non-digit is encountered. (Or as soon as it is clear that the number denoted by ⟨\mycommand's argument⟩ is too big. In this case you are informed via a low-level TeX error message.) After the assignment is performed, TeX is after the assignment and therefore the token \get@args is inserted right before the first token which in the course of gathering the ⟨number⟩ of the assignment is considered to not be a component of that ⟨number⟩.
In case ⟨\mycommand's argument⟩ (after expansion) either yields emptiness or consists only of digits that don't form a number that is too big, this is the first token \hfuzz coming from the ⟨replacement text⟩ of \mycommand.
Then \get@args grabs everything up to the first token \hfuzz as its first \hfuzz-delimited argument and ⟨\mycommand's argument⟩ as its second argument delimited by the second token \hfuzz. Therefore, in case ⟨\mycommand's argument⟩ in the course of gathering the tokens of the ⟨number⟩ for the \count@-assignment did not yield emptiness or only digits, \get@args's first argument is not empty. (Emptiness is tested via \if\relax\detokenize{\get@args's 1st argument⟩}\relax⟨empty⟩else⟨not empty⟩\fi.)
In this case \get@args's second argument, which holds ⟨\mycommand's argument⟩ is used for delivering ⟨\mycommand's argument⟩ is not a number. In case \get@args's first argument is empty, gathering tokens for the ⟨number⟩ of the assignment did not lead to leaving things that are not a component of a ⟨number⟩ and you get ⟨\mycommand's argument⟩ is a number\addtocounter{sum}{⟨\mycommand's argument⟩}.
The test is not totally safe.
E.g., the test assumes 0 in case ⟨\mycommand's argument⟩ is blank, which, however, is not necessarily to be considered undesired/erroneous behavior.
E.g., the test fails in case ⟨\mycommand's argument⟩ expands to digits trailed by the token \hfuzz.
E.g., the test fails in case expanding ⟨\mycommand's argument⟩ in the course of gathering tokens belonging to the ⟨number⟩ leads to attempting to expand things where attempting expansion yields error messages (e.g. undefined tokens, unbalanced \if../\else/\fi, unbalanced \csname/\endcsname, \the trailed by s.th. that is not an ⟨internal quantity⟩,…).
E.g., the test fails in case expanding ⟨\mycommand's argument⟩ in the course of gathering tokens belonging to the ⟨number⟩ leads to triggering expansion-cascades by things like \expanded/\romannumeral/\the/\if/\number etc which remove/rearrange some of the subsequent tokens \hfuzz⟨\mycommand's argument⟩\hfuzz, so that usage of \get@args does not match its definition…).
E.g., the test fails in case expanding ⟨\mycommand's argument⟩ tricks TeX into some sort of tail-recursive loop which either never ends or at some stage ends with a low level error message about TeX's memory capacity being exceeded or the number being too big or the like as would be the case, e.g., with things like \mycommand{3\NastyMacro} when \NastyMacro is defined as \def\NastyMacro{0\NastyMacro} or \def\NastyMacro{\NastyMacro0} or \def\NastyMacro{\NastyMacro 1} or \def\NastyMacro{1\NastyMacro}.

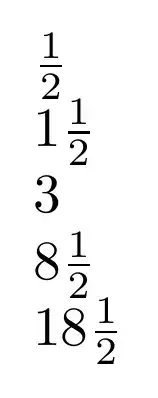
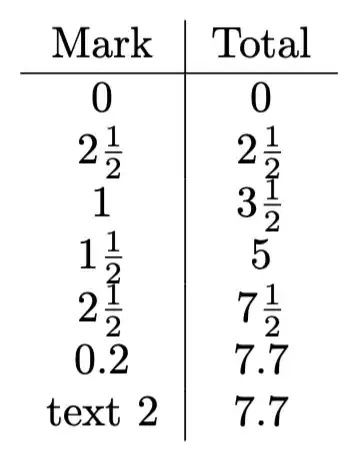

FIX MARKS, but this could easily be changed to whatever we wanted (including#1). – rbrignall Mar 15 '24 at 17:20