Puzzle: How to compute Bringhurst's page style with TeX/Metapost/TikZ etc

Question

In his book The Elements of Typographic Style, Bringhurst presents a hexagonal pattern for geometrically constructing the elements of the page layout.

Question: Can the dimensions be simply extracted geometrically using TikZ, tkz-eu­clide, Metafont/post, or similar LaTeX packages? (Geometric elegance is key here, not just a brute force solution demonstrating that TeX is turing complete, and hence can solve the implicit problem.)

I originally thought that this would be a great example of the geometric methods available through, for example, tkz-eu­clide, but have been unable to come up with an explicit construction. Of course, one can follow the construction through to obtain an implicit set of equations with a unique solution which I have used to calculate the parameters in the following code, but can one solve the problem elegantly using the geometric methods found in these packages?

\documentclass{standalone}
\usepackage{tikz}
\usepackage{tkz-euclide}
\usetikzlibrary{decorations.pathmorphing}

\begin{document}
\begin{tikzpicture}[scale=5.2in/1cm/2]
    \path (0,0) coordinate[label=below:{ll}] (ll)
    -- (1,0) coordinate[label=below:{lr}] (lr)
    -- ++(60:1) coordinate[label=right:{r}] (r)
    -- ++(120:1) coordinate[label=above:{ur}] (ur)
    -- ++(180:1) coordinate[label=above:{ul}] (ul)
    -- ++(240:1) coordinate[label=left:{l}] (l)
    -- ++(300:1) coordinate (ll);
    \coordinate[label=below right:{a}] 
                  (a) at (1.27106916798686, 0.469505571318668);
    \coordinate (tll) at (0.117300021398114, 0.294835256924744);
    \coordinate (tlr) at (0.798192881206518, 0.294835256924744);
    \coordinate (tur) at (0.798192881206518, 1.61553741320908);
    \coordinate (tul) at (0.117300021398114, 1.61553741320908);
    \coordinate[label=below:{x}] (x) at (0.435936138301, 0);
    \coordinate[label=above:{y}] (y)   at (0.689095323638, 1.73205080756888);
    \tkzInit[ymin=0,ymax=2,xmin=-0.5,xmax=2]
    \tkzInterLL(l,ur)(a,ul) \tkzGetPoint{A}
    \tkzInterLL(ll,y)(ul,a) \tkzGetPoint{B}
    \tkzInterLL(l,ur)(ll,y) \tkzGetPoint{C} 
    \tkzInterLL(ll,a)(l,x) \tkzGetPoint{D}
    \tkzDefCircle[in](A,B,C) \tkzGetPoint{U} \tkzGetLength{rU}
    \tkzDefCircle[in](tll,tlr,D) \tkzGetPoint{L} \tkzGetLength{rL}

    % Locate page number
    \tkzDefShiftPoint[L](1,0){Lr}
    \tkzInterLL(L,Lr)(tur,tlr) \tkzGetPoint{pagenumber}

    % Locate running header
    \tkzDefShiftPoint[U](0,\rU pt){Uu}
    \tkzDefShiftPoint[Uu](1,0){Uur}
    \tkzInterLL(Uu,Uur)(y,r) \tkzGetPoint{header}

    \color{black};
    \draw (ll) -- (lr) -- (r) -- (ur) -- (ul) -- (l) -- cycle;
    \color{gray};
    \draw (ur) -- (l) -- (x) -- (r) -- (y) -- (ll) -- (a) -- (ul);
    \draw (l) -- (ur);
    \draw (tul) -- (tur) -- (tlr) -- (tll) -- cycle;
    \draw (ul) -- (ur) -- (lr) -- (ll) -- cycle;

    \tkzSetUpLine[color=gray]
    \tkzDrawCircle[R](U, \rU pt)
    \tkzDrawCircle[R](L, \rL pt)
    \tkzDrawSegments(Uu,header L,pagenumber)
\end{tikzpicture} 
\end{document}

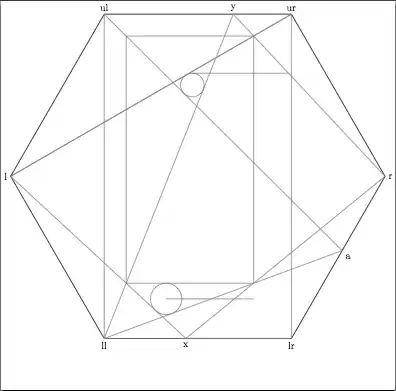
Update: To clarify the problem, in addition to the intersection constraints implicit in the picture, one must also impose that the textblock be rectangular with strict vertical/horizontal orientation. This, along with the constraints that the points lie within the hexagon (not somewhere outside) are enough to ensure that the solution is unique up to an overall scaling that is fixed by the roughly 5.2"x9" physical paper size used for Bringhurst's book. (As mentioned by @percusse, the hexagon gives an exact ratio 5.2:5.2*2*cos(30º) = 5.2:9.006664202....)

The construction can be completely specified with simple geometric intersections etc. if two numbers are specified. In particular, one can specify the fraction y along ul--ur and x along ll--lr (z.y=y[z.ul,z.ur] and z.x=x[z.ll,z.lr] in metapost notation).

The exact solution can be found algebraically to be:

q = (81 - √3186)^(1/3)
y = q/3 - 2 + 5/q ≈ 0.689095323637659465372247907...
x = (y^2 + 4*y + 3)/(-2*y^2 - 4*y + 18) ≈ 0.4359361383008273751170828497...

Additional consistent solutions exist, but the points x and y lie outside of the corresponding sides of the hexagon: this is the unique solution with the textblock lying within the page. Since these are solutions of cubic equations, I have my doubts that a complete solution lies within the linear solving abilities of Metapost, but think there still might be a nice geometric construction.

Reference: This answer to the question: Bringhurst chapter style in memoir

Answer 1

Just to get the ball rolling (and to get to play with MetaPost), here is what I have so far: (updated with a few ideas I had, I still need to test out Barbara’s and mforbes’ hints and ideas)

beginfig(1);
  defaultscale := .8; % make the text a little smaller
  u := 1.5in;
  phi := 1.618033988749895;

  for i:= 0 upto 5: z.hexc[i] = right scaled u rotated (i*360/6); endfor;
  path hexa; hexa := for i:=0 upto5: z.hexc[i]--endfor cycle;
  fill hexa withcolor .9[green,white]; draw hexa;
  dotlabel.rt("r", z.hexc0); dotlabel.urt("ur", z.hexc1);
  dotlabel.ulft("ul", z.hexc2); dotlabel.lft("l", z.hexc3);
  dotlabel.llft("ll", z.hexc4); dotlabel.lrt("lr", z.hexc5);

  path recto; recto := z.hexc1--z.hexc2--z.hexc4--z.hexc5--cycle;
  path verso; verso := recto shifted (-1u,0);
  for i:=verso,recto:%,recto shifted (1u,0):
    draw i withpen pencircle scaled 1.2; endfor;

  picture mforbes; mforbes :=
  image(
    z.a   = (1.27106916798686u, 0.469505571318668u);
    z.tll = (0.117300021398114u, 0.294835256924744u);
    z.tlr = (0.798192881206518u, 0.294835256924744u);
    z.tur = (0.798192881206518u, 1.61553741320908u);
    z.tul = (0.117300021398114u, 1.61553741320908u);
    z.x   = (0.435936138301u, 0);
    z.y   = (0.689095323638u, 1.73205080756888u);
    dotlabels.lrt(a,tll,tlr,tur,tul,x,y);
  );
  drawoptions( withcolor .5 red );
  draw mforbes shifted llcorner recto;

  % Bringhurst's lines:
  draw z.hexc1--z.hexc3--z.x shifted llcorner recto--z.hexc0--
    z.y shifted llcorner recto--z.hexc4--z.a shifted llcorner recto--z.hexc2
    %dashed evenly
    ;
  drawoptions();

  % Van de Graaf: http://en.wikipedia.org/wiki/Canons_of_page_construction
  picture van_de_Graaf; van_de_Graaf := image(
    path Van_de_Graaf[];

    Van_de_Graaf0 := ulcorner verso--lrcorner recto--ulcorner recto
      --llcorner verso--urcorner recto;
    draw Van_de_Graaf0 dashed evenly;

    % subpath (0,1) is the first line, (1,2) is the second, etc.
    z.vdG0 = (subpath(3,4) of Van_de_Graaf0) intersectiontimes
      (subpath(3,4) of hexa);
    z.vdG1 = point xpart z.vdG0 of subpath(3,4) of hexa; % show this point
    z.vdG2 = point ypart z.vdG0 of subpath(1,2) of hexa; % on this path
    % ypart(z.vdG1) == xpart(z.vdG1) ?
    dotlabel.lft("vdG1", z.vdG1);
    dotlabel.urt("vdG2", z.vdG2);
    % Close, but no cigar. Back to the drawing board.

    % van de Graaf continued to project lines from the intersections:
    z.vdG3 = (subpath(1,2) of Van_de_Graaf0) intersectionpoint
      (subpath(3,4) of Van_de_Graaf0);
    z.vdG4 = (xpart z.vdG3, ypart urcorner recto);
    z.vdG5 = (subpath(0,1) of Van_de_Graaf0) intersectionpoint
      (subpath(2,3) of Van_de_Graaf0);
    z.vdG6 = (xpart z.vdG5, ypart urcorner verso);
    dotlabels.ulft(vdG3, vdG4, vdG5, vdG6);
    Van_de_Graaf1 := (z.vdG5)--(z.vdG4);
    Van_de_Graaf2 := (z.vdG6)--(z.vdG3);
    drawoptions( dashed evenly );
    draw Van_de_Graaf1; draw Van_de_Graaf2;
    drawoptions();
    % Nope. Not even close.

    z.guess_a = whatever[z.vdG6,z.vdG3] = whatever[z.hexc0,z.hexc5];
    % Did I hit it? Pleasepleasepleasepleaseplease...
    dotlabel.lrt("guess a", z.guess_a);
    % Nope.

    % That intersection of cross-page vdG's looks promising
  );
  draw van_de_Graaf withcolor .5 white;

  z.golden1 = point 1/phi of subpath(5,4) of hexa;
  z.golden2 = point 1/phi of subpath(2,1) of hexa;
  drawoptions( withcolor .5[green,red] );
  dotlabel.bot(btex $\phi$ etex, z.golden1);
  dotlabel.top(btex $\phi$ etex, z.golden2);
  drawoptions();

endfig;
end

(I haven't used MetaPost much, so if you have suggestions on improving, please share)