The following quote is from "Oblique Flying Wings: An Introduction and White Paper" from Desktop Aeronautics, Inc., available at https://www.desktop.aero/library/ofwwhitepaper.pdf.
2.2.2 Effect of Oblique Sweep on Spanwise Lift Distribution
A well-known effect of wing sweep is the variation of induced downwash
along the span from the trailing wake that produces an additional lift
distribution characterized by increased loading on the aft wing and
reduced additional lift on the forward wing. For a wing with no twist
or bend, this results in a significant rolling moment, tending to roll
the forward wing downward. There is also a yawing moment from the
asymmetrical distribution of induced drag that tends to unsweep the
wing.
Keep in mind that by "wing sweep" the authors are talking about obliquely sweeping both wings together as a unit, like in the photo in this other answer to the present question. We have essentially the same effect when we sideslip. The direction of the roll torque generated is toward the "forward" wing, which in a sideslip is the "upwind wing". In a steady-state non-turning sideslip this would also be the "lowered" wing. This is an anhedral-like effect.
In the paper they recommend adding a small amount of dihedral to the outboard portions of an oblique-wing aircraft to counteract this, with the amount of dihedral being dependent on the lift coefficient that the aircraft is intended to fly at.
I'd suggest that this effect due to "the variation of induced downwash along the span" falls within the scope of the question's focus on "tip vortices".
The anhedral-like (upwind) roll torque generated by an unswept, zero-dihedral wing in a sideslip was also the subject of a post on an aerodynamics subforum of the"RCGroups" model-airplane on-line forum by a prolific, knowledgeable contributor with the username "ShoeDLG". Some excerpts from his post:
I used a Vortex Lattice Method to explore the impact of various
Radian Pro wing design features on apparent dihedral effect.
The cases I looked at (all without any twist):
- Untapered / Unswept / Zero Dihedral Wing (flat AR 10 rectangular wing)..."
and then
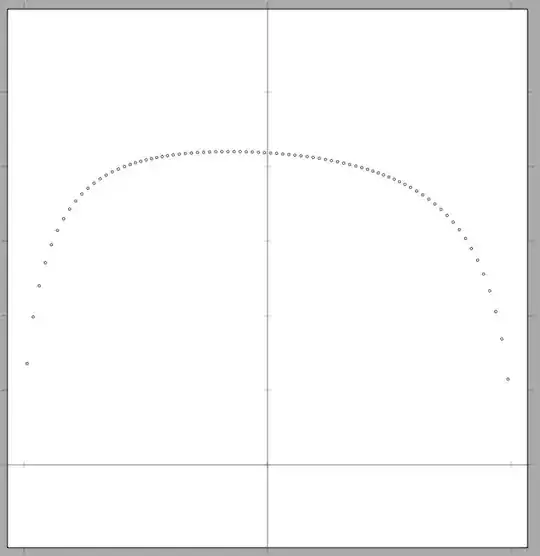
The results are shown in the first attachment. A couple of
observations:
- A flat rectangular AR 10 wing has negative apparent dihedral effect at positive AOA and positive apparent dihedral effect at negative
AOA..."
and then
The dihedral effect associated with an untapered, unswept, zero
dihedral wing is interesting. The span loading for an AR 10
rectangular wing at 5 degrees AOA and 20 degrees sideslip (to
exaggerate the asymmetry) is shown in the second attachment."
These conclusions are consistent with the "Oblique Flying Wings" white paper-- during a sideslip, on an aircraft with flat (no dihedral or anhedral) wings with no sweep, the lift distribution is changed in a way that creates an "upwind" roll torque-- i.e. an anhedral-like effect.
Here are the two attachments:

However, a web page called www.flightlab.net by Bill Crawford came to the opposite conclusion, stating that during a sideslip, tip vortices shifted in a way that increased the angle-of-attack of the upwind wing and decreased the angle-of-attack of the downwind wing, contributing a dihedral-like roll torque component, toward the downwind wing. A full page of text devoted to the topic, along with an illustration, may be seen on page 14 of his generally excellent PDF "Flightlab Ground School: 4. Lateral/Directional Stability", now viewable only on this link on the Wayback Machine. This content is well worth reading through.
Crawford goes on to reach the following conclusion: (footnotes added)
"Since downwash strength is a function of CL, pulling or pushing on
the stick will affect roll moment due to sideslip in a manner similar
to the swept-wing example already described.1 (Our trainers’
rectangular planforms tend to promote strong tip vortices. Other
straight-wing planforms with different lift distributions might not be
as effective.)"
followed by:
From all the above, an under-appreciated yet nevertheless great truth
of airmanship emerges: For a swept or a straight wing, pulling the
stick back tends to increase rolling moments caused by sideslip (and
by yaw rate), pushing decreases them.
(In the specific case of an unswept wing, Crawford is obviously assuming that there is some aspect of the aircraft's overall geometry, such as a high wing position, or actual dihedral, or perhaps just the tip vortices themselves, that results in an overall dihedral-like roll torque during a sideslip. The comment above wouldn't make sense for, say, a low-wing airplane with no sweep and a great deal of actual anhedral, because then the effect that he is claiming for the wingtip vortices, which are most pronounced at high Cl, would be acting in the wrong direction.)
So Crawford is reaching the opposite conclusion on the effect of tip vortices on the balance of roll torque during a sideslip than the other sources cited above-- he is claiming that they contribute a dihedral-like roll torque component, toward the downwind wing. I can't account for this discrepancy at present. Is it possible that Crawford's conclusions are valid for wings of a certain geometry, such as the low-aspect ratio wings with broad wingtips found on many trainers? Or is he simply mistaken in the idea that tip vortices, and the associated larger upwash / downwash flow field around the wings, tend to contribute a dihedral-like, downwind roll torque component during a sideslip? Should his observation of increased rolling moments due to sideslip at high lift coefficients versus at low lift coefficients, even in unswept wings, be explained by other means entirely?
Footnotes:
- I.e. adding to the dihedral-like roll torque that would be created by sweep


