Planetary system simulation with real orbital datas

Question

When making a planetary system, I'd like to respect the eccentiricity of orbits (elliptical orbits), using the facts supplied by astronomical data centers like here: http://www.icoproject.org/data.html ?

One of the focus of the ellipse can be set at the center of the planetary system; i.e.the center of the central star.

I have other parameters under control (e.g.speeds, orbits inclinations, period of rotation...).

Thanks in advance for your precious advices!

There is a question mark in your post but there is no query. Could you clarify what your question is? — Duarte Farrajota Ramos, Feb 26 '19 at 12:48

batFINGER · Accepted Answer · 2020-08-04T11:28:35.133

Orbital Eccentricity - Wikipedia

For elliptical orbits, a simple proof shows that arcsin(e) yields the projection angle of a perfect circle to an ellipse of eccentricity e. For example, to view the eccentricity of the planet Mercury (e = 0.2056), one must simply calculate the inverse sine to find the projection angle of 11.86 degrees. Next, tilt any circular object (such as a coffee mug viewed from the top) by that angle and the apparent ellipse projected to your eye will be of that same eccentricity.

Via the UI, add a primitive circle mesh or curve, rotate about X RX 11.86, then scale in 0 in Z, S Z 0

Result of running test script

Quick test script, creates a circle, rotates by projection angle about X, projects onto XY plane by setting z to 0.

Could use bmesh, or make the projection matrix.

import bpy
import bmesh
from mathutils import Matrix
from math import asin
def elliptic_orbit(name, e, context=bpy.context):
    bpy.ops.mesh.primitive_circle_add()
    R = Matrix.Rotation(asin(e), 4, 'X')
    ob = context.object
me = context.object.data
ob.name = me.name = &quot;%s_orbit&quot; % name
me.transform(R)
for v in me.vertices:
    v.co.z = 0
me.update()


elliptic_orbit("Earth", 0.017)
elliptic_orbit("Mercury", 0.2056).scale = 0.387

elliptic_orbit("Venus", 0.007).scale = 0.723
elliptic_orbit("Mars", 0.093).scale = 1.524 
elliptic_orbit("Jupiter", 0.048).scale = 5.203 
elliptic_orbit("Saturn", 0.056).scale *= 9.555

Alternatively orbit as a curve. Here I've used a scale matrix to scale z component to zero, could do same in mesh version.

def elliptic_orbit(name, e, context=bpy.context):
    bpy.ops.curve.primitive_nurbs_circle_add()
    S = Matrix.Scale(0, 4, (0, 0, 1))
    R = Matrix.Rotation(asin(e), 4, 'X')
    ob = context.object
cu = context.object.data
ob.name = cu.name = &quot;%s_orbit&quot; % name
cu.transform(R)
cu.transform(S)

return ob

For compatability sakes I've applied the transforms sequentially. For 2.5 K= verson < 2.8 could use cu.transform(R * S) and for 2.8 cu.transform(R @ S)

Ellipse foci

Ellipse - Wikipedia

shape parameters: a: semi-major axis, b: semi-minor axis c: linear eccentricity, p: semi-latus rectum.

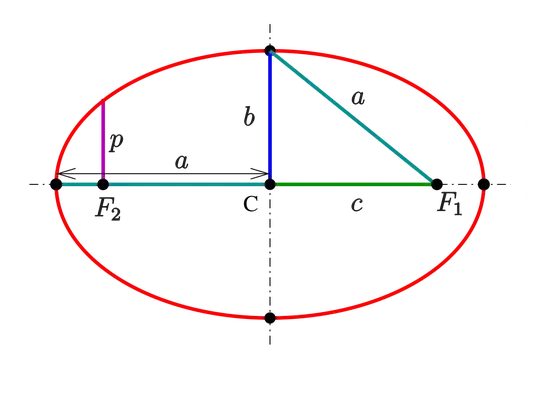
By Ag2gaeh - Own work, CC BY-SA 4.0, Link

The semi-major axis will lie on the rotated axis X. c the linear eccentricity can be calculated thus

>>> ob = C.object
>>> ob.name
'Jupiter_orbit'
>>> ob.dimensions.xy.length
0.4994825301958152

The two foci are F1, F2 = (c, 0, 0), (-c, 0, 0)

May find the following post on barycentric orbits of interest.

Planetary system simulation with real orbital datas

1 Answers1

Linked