Can you animate objects using differential equations?

Question

I am looking for a software to animate biological processes based on differential equations, and I was wondering if Blender would work for something like this.

Answer 1

Many differential equations can be solved and animated using animation nodes. For example, the equations for a mass on a spring with a damper were used to animate this cube.

This example is at

---

Overview

• Differential equations can be simulated, frame by frame in an animation, if they are in the form of a 1st order, ordinary differential equations. See an example of forming 1st order ODEs at Example.
• Once in the form of a 1st order ODE, simulation consists of calculating the change in state when the frame changes.
• The state is used to change some aspect of the animation, like the position.
• This can be done by saving the state in a text block, and at each frame change, updating the text block by solving the differential equations.
• The animation nodes add-on makes it relatively simple to implement this.

---

Detailed steps:

1. Start with the differential equations. Arrange as 1st order differential equations. The equations for a spring-mass-damper are . By rearranging this equation into a 1st order differential equation, this is easily simulated. The 1st order differential equations for the mass spring damper are below. These equations show that the change in velocity is a function of the spring force and the damping force. The change in position is a function of the velocity.

   • 
   • 

2. If not already installed, install the animation nodes add on. See Animation Nodes on GitHub

3. Create a new Blender file.

4. Create two text blocks. Name them 'IC' and 'state'. Add the initial condition for the equations in to the 'IC' block.

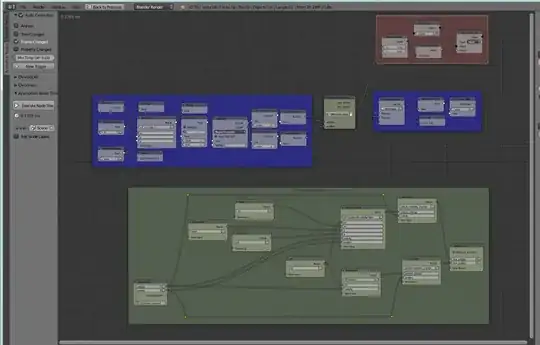
5. Open up the node editor and create the following animation node setup. The setup is explained below. This setup consists of 4 major parts. A part to read the state from the data blocks, a part to write the new state, a apart to solve the equations for one frame, and a part to update the animation.

6. The part that reads the state from the text block includes logic to determine if the animation just started. If the frame number is 1, then the initial conditions are used for the equations. Otherwise, the last stored state is used. The contents of the blocks is converted to numbers to work with the equations.

7. The differential equations are solved in this part. These equations mirror the equations in step #1 with some modification to solve the differential equation (see euler method). The time step (dT) for each frame is used to determine how much the position and velocity change. These changes are added to the prior position and velocity.

8. The updated state is written to the 'state' datablock.

9. To have the animation affected, the animation nodes take the position variable and use it to change he position of the cube.

---

The blend file with this example is located at

Answer 2

You can also write some Python script that writes its outcome to an fcurve. It can evaluate the differential equation, look up the value from the previous frame in the fcurve, add the two together, and write the result to the current frame.

Answer 3

You can do this by using curve modifiers. As soon as you set a keyframe on any property, it will show up in the graph editor. All channels in the graph (f-cuves) can be manipulated with modifiers. Try the generate modifier for example, you can put equations there.

https://docs.blender.org/manual/ko/dev/editors/graph_editor/fcurves/fmodifiers.html