4

I have read many excellent answers to similar questions, but never one this specific. Here is another way to ask it.

  • Why is the modulation transfer function (MTF) of $\textrm{rect}(x/5) = \textrm{sinc}(5x)$ not equal to the DFT of a vector of zeros with 5 ones in the center?

Relative MATLAB picture and code: 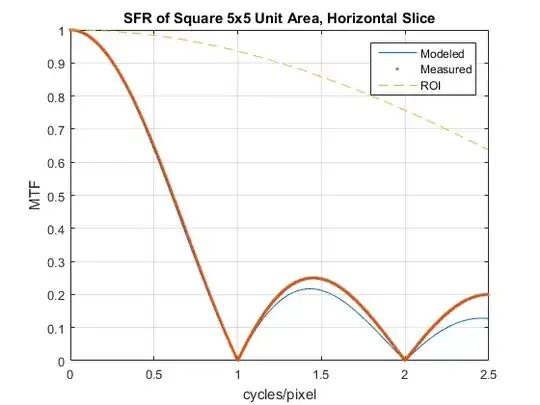picture

x = -512:511; x = x / 1024;
sq = zeros(1,1024); sq(511:515) = 1;
sqMTF = abs(sinc(x*5));               %'Modeled'
sqDFT = 1/5* abs(fftshift(fft(sq)));  %'Measured'

I can make the two curves overlay each other by multiplying the DFT result by $\textrm{sinc}(x)$, which I intuit should be related to windowing of the original signal and related spectral leakage.

  • But shouldn't this be a convolution in the frequency domain, as opposed to a multiplication?

Jack.

Community
  • 1
Jack Hogan
  • 53
  • 1
  • 7

2 Answers2

3

The difference is between $\mbox{sinc}$ and the periodic version obtained using the DFT.

See this answer for a comparison.

It strikes me that asinc = ratio of two sincs.

The $\mbox{asinc}$ function is a ratio of two $\sin$ functions: $$ \frac{\sin(N\omega/2)}{\sin(\omega/2)} = \frac{\sin(N\omega/2)}{\omega/2} \frac{\omega/2}{\sin(\omega/2)} $$ so, yes, you could see it as the ratio of two $\mbox{sinc}$ functions.

Underlying question: can I model the sampling of a continuous signal (by, say, a digital camera) in the frequency domain as the DFT of the signal convolved with a Dirac delta train times the DFT of the pixel footprint (a rect)? If so, why is the DFT of the pixel footprint an asinc instead of a sinc?

So you seem to be trying to model taking a picture with a digital camera? Camera modeling is a little tricky. Even Gonzales and Woods seem to gloss over it.

The fundamental issue is the DFT of a $\mbox{rect}$ ($\Pi$) is a $\mbox{asinc}$.

If you're doing a discrete-time Fourier transform (DTFT), then it's not, but usually when dealing with computed FTs, you want the DFT.

Community
  • 1
Peter K.
  • 25,714
  • 9
  • 46
  • 91
  • Thanks Peter. So I gather that sampling continuous rect(x/5) produces an asinc function via DTFT in the frequency domain. Is that what it would also yield via DFT? (Indulge me, I am a photographer, not a scientist;-) It strikes me that asinc = ratio of two sincs. Underlying question: can I model the sampling of a continuous signal (by, say, a digital camera) in the frequency domain as the DFT of the signal convolved with a Dirac delta train times the DFT of the pixel footprint (a rect)? If so, why is the DFT of the pixel footprint an asinc instead of a sinc? – Jack Hogan May 22 '16 at 13:19
  • @JackHogan I have a busy day today, so will try to answer tonight. – Peter K. May 22 '16 at 15:24
  • 'Preciate it Peter. – Jack Hogan May 24 '16 at 11:30
1

Computing a DFT requires an input consisting of a finite length of samples instead of a infinite continuous function.

Because the full spectrum (FT) of a rect function is not bandlimited to below half the sample rate, aliased images will appear in the DFT of any finite window of samples of this non-bandlimited rect. The sum of all these aliased images folded (or wrapped around) into a finite DFT result window is a Dirichlet function, or periodic Sinc, which differs from a single Sinc by a denominator of sin(W) instead of W.

The aliasing will be due to the sampling of a non-bandlimited signal, no matter what the DFT length. However a longer DFT window will spread out the train of aliased images in terms of DFT result bins, thus changing the denominator to where sin(W) is closer to W.

A bandlimited version of a rect (allowing sampling without aliases) will not be a sequence of ones surrounded by zeros.

hotpaw2
  • 35,346
  • 9
  • 47
  • 90
  • Thanks hotpaw2. From what I understand the asinc is the ratio of my sinc(5x) to sinc(x). Could the sinc(x) term be related to the finite window over a non-periodic signal in the spatial domain fed to a DFT? If so how? – Jack Hogan May 22 '16 at 13:35