How to sample a complex function?

Question

We know that we can sample a real function such as g(x) = sin(2pi*f*x) with a (approximate) critical sampling rate expressed as max[dg(x)/dx/pi] = 2f, assuming that x in the range of [-x0,x0]. But what's the critical sampling frequency of a complex function, such as g(x) = cos(a*x^3)*exp(i*2pi*f*x) (here 'a' is a constant)? I try to analyse it in a similar manner by separating g(x) into the real and imaginary parts, or alternatively the modulus and phase parts, but I feel the two approaches are both unreasonable.

Answer 1

It is the same requirement. Note that the digital spectrum is the convolution of the input analog spectrum and the sampling spectrum, such that the analog spectrum is replicated at every multiple of the sampling rate $f_s$. (The sampling process is the multiplication in time with an train of impulses, the FT of a train of impulses in time is a train of impulses in frequency. Multiplication in time is convolution in frequency.

Thus the case for a real analog signal would appear as follows:

And the case for a complex analog signal would appear as follows:

For the case of the real input, the unique digital spectrum extends from $f=0$ to $f=f_s/2$ in the "first Nyquist zone" since the spectrum is complex conjugate symmetric, so the negative frequencies are redundant. However in the case of a complex input, the unique digital spectrum extends from $-f_s/2$ to $+f_s/2$ in the first Nyquist zone. In both cases the minimum sampling rate is twice the highest frequency of such lowpass signals. The bandwidth may be specified as a one-sided or two-sided bandwidth which if not clarified can lead to some confusion.

What is necessary with regards to practical implementation, is the use of two A/D Converters instead of one: one to sample the real and the other to sample the imaginary, but the sampling rate needed for both would be identical as illustrated above. Further, prior to sampling in either case (real or complex), there should be an anti-alias filter to limit the bandwidth including noise as detailed in this post.

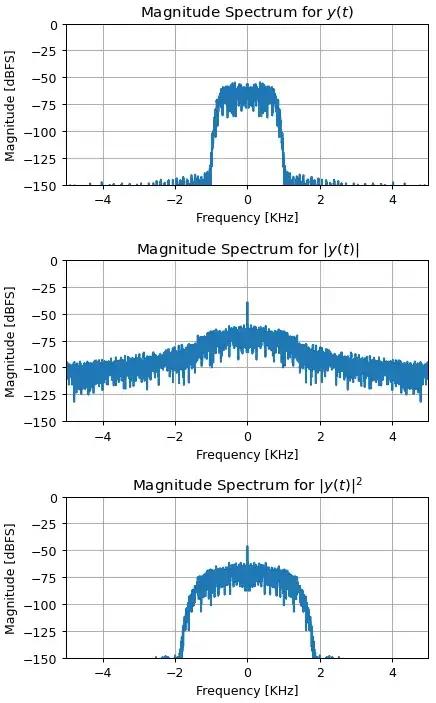
To sample the magnitude and phase (instead of real and imaginary), we note that the magnitude and phase are each independent of each other (just as the real and imaginary components are for a complex waveform) but the maximum frequency of the magnitude and phase is unbounded. However interestingly note that the maximum frequency of magnitude squared is bounded. I demonstrate this using a randomly generated bandlimited waveform in the spectrum plots below. Thus if magnitude is to be used, it should be squared prior to sampling and then the sampling rate should be doubled to support the increase in occupied bandwidth. I do not know a similar operation that can create a bandlimited phase; further phase modulation is non-linear with sidebands given by Bessel functions for sinusoidal modulation; this suggests the frequency content of the phase for an arbitrary waveform will decrease to insignificance in a practical sense, but that rolloff vs frequency is relatively slow (for that reason I would not recommend sampling magnitude and phase versus real and imaginary for a complex waveform).

Answer 2

On a computer, under the hood, complex values are stored as two separate real values! This is doable because real and imaginary are completely independent. Hence, you can analyze them separately.

For a perspective, what's the sampling requirement for a purely imaginary signal? You should conclude, there's no difference. An answer:

"Sufficient sampling rate" means "enough to capture signal's variability", and "variability" is about the shape of $x(t)$; from variability's point of view, $j \cdot x(t)$ is same as $2\cdot x(t)$, that is, multiplying by a constant. Put differently, it only matters that a sine has twice the wiggles of another sine.

So if you can accept $f_{sA}$ is the required sampling rate for $A(t)$ and $f_{sB}$ for $B(t)$, then you should accept for $A(t) + B(t)$ it's $\text{max}(f_{sA}, f_{sB})$, which is exactly how it works with complex, except $B(t)$ is like $j\cdot b(t)$.

That's to avoid aliasing. For preserving information, it's a little more complicated, but let's leave it here. Note that above is informal intuition that happens to be accurate, not precise justification.

Re & im vs modulus & phase, formalities

Analyzing real and imaginary separately and taking the maximum $f_s$ is one way. Formally, the max required sampling rate is simply double the highest non-zero frequency of the continuous Fourier transform; problem is, this approach isn't practical, there's better ways (TLDR keep increasing sampling rate until DFT has negligible energy near Nyquist).

You're correct to think there's complications from modulus standpoint: indeed, the required sampling rate for modulus of vast majority of signals is, strictly, infinite, but roughly, double the original signal's to capture most energy. That's for reals - for complex, if it's a bandpass signal, for preserving information, it'd be twice the bandwidth - but for avoiding aliasing, it's just the bandwidth (max freq minus min freq), but that's almost always much less than twice the original sampling frequency!

From phase standpoint, there's serious numeric limitations per float division involved, and the approach is impractical.

More importantly, modulus and phase will almost never yield the strictly correct $f_s$, though I'm unsure on rough correctness. A simple example is $\sin(2\pi 2 t)$ that requires $>4\text{Hz}$, yet its modulus requires $\infty$. This may seem contradictory, but really, modulus and phase are themselves signals, they just happen to also describe the original signal in their own ways.

Code example

First, to repeat, generally phase cannot be reliably recovered in float computations. Interestingly, however, for the purposes of this question, it is exact - in that the convolution of spectra of $|x(t)|$ and $e^{j\phi(t)}$ in $x(t)=|x(t)|e^{j\phi(t)}$ can be used to determine $f_s$ of $x(t)$. Demo:

for N in (16, 17, 1000000, 10000001):
    x = np.random.randn(N) + 1j*np.random.randn(N)
    xa = np.abs(x)
    xp = np.unwrap(np.angle(x))
    xrec = xa * np.exp(1j * xp)
    assert np.allclose(xrec, x)

But because xp is unreliable, it can easily overestimate the true fs. And since xa's spectrum is almost always greatly expansive, it's also a poor predictor. Lastly, spectrum of $|x(t)|^2$ may be of greater interest.