The relationship is convolution: the magnitude squared in the time domain is the complex conjugate product as demonstrated below for the case of continuous time $x(t)$:
$$|x(t)|^2 = x(t)x^*(t)$$
Such a product in time is convolution in frequency. The spectrum of $x^*(t)$ for the CTFT (or $x^*[n]$ for the DFT) is mirrored of that for $x(t)$ and $x[n]$ but otherwise identical in terms of spectral occupancy. For this reason the resulting spectrum will be bounded to twice the bandwidth of time domain waveform (for the case of the DFT, this means the spectrum of $x[n]$ must have a spectral occupancy that is less than $N/2$ samples otherwise the result will fully occupy the DFT with additional distortions due to the spectral overlap.)
That said the relationship for the DFT (FFT) would be:
$$\texttt{FFT}\{ x[n] x^*[n] \} = X[k] \circledast X^*[-k]$$
Where the symbol $\circledast$ above represents a circular convolution, which conveniently can be determined from the FFT and IFFT using the following well known relationship (this is used for “fast convolution” or equivalently when one of the FFT results is itself conjugated “fast correlation”):
$$C[k] =\texttt
{IFFT} \big[\,\texttt{FFT}(X[k])\,\texttt{FFT}(X^*[-k])\,\big]$$
Note- that if we rewrite the above known relationship to equivalently be the fft of the product of the inverse fft’s we get the original time domain result further showing this relationship!
$$\texttt{FFT}\{ x[n] x^*[n] \} =\texttt
{FFT}\big[\,\texttt{IFFT}(X[k])\,\texttt{IFFT}(X^*[-k])\big]$$
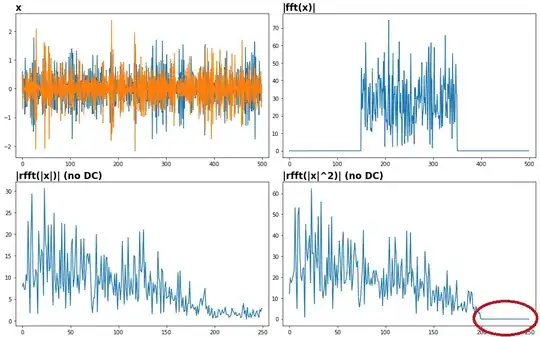
x, the|x|was a distraction – OverLordGoldDragon Mar 06 '23 at 15:10